Vítejte! Tato stránka slouží jako databáze řešených fyzikálních úloh pro střední a základní školy.
▮
Na Milešovku a zpět
#8,
Marek Scholz (admin),
pos:/9,
kat
Anakin každé ráno leze na Milešovku, aby se podíval zblízka na oblaka. Cestou nahoru jde rychlostí 3 km/h, nahoře se hned otočí a cestou dolů běží rychlostí 6 km/h. Jaká je jeho průměrná rychlost na celé trase?
Řešení: Nesmíme se nechat zmást a tipnout, že průměrná rychlost je 4,5 km/h - tak to není. Průměrná rychlost je rovna "celková dráha" / "celkový čas". Délku jednosměrné cesty na Milešovku si můžeme zvolit libovolnou, výsledek bude na této volbě nezávislý. Volme třeba 1 km. Potom $v_p = 2 / (1/3 + 1/6) = 2 / (0,5) = 4\,\text{km/h}$. Můžeme si všimnout, že výsledek je harmonickým průměrem zadaných rychlostí.
Výsledek: 4 km/h
Hint: Je potřeba spočístat celkovou dráhu a celkový čas.
ID: 8;
Tags: průměrná rychlost;
Autor: Marek Scholz (admin);
Position: /9;
▮
Cipísek honí Rumcajse
#9,
Marek Scholz (admin),
pos:/9,
kat
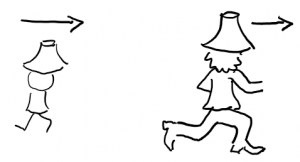
Rumcajs vyběhl ze zámku a běží rychlostí 5 m/s. Za 10 minut po něm vyběhl Cipísek, který má mladé hnáty a běží rychlostí 8 m/s. Jak daleko od zámku Rumcajse dohoní? Řešte početně i graficky!
obr.
skrýt |
S |
M |
L
Řešení: Rumcajs má náskok 10 minut=600 s a za tuto dobu uběhne 3000 m. Vzájemná rychlost Cipíska a Rumcajse je 8-5 = 3 m/s. Touto rychlostí bude Cipísek ukrajovat Rumcajsův náskok a bude mu to trvat zřejmě 1000 s, čili 16 minut a 40 sekund. Cipísek běží od zámku po dobu 1000 s rychlostí 8 m/s a tedy Cipísek Rumcajse dohoní 8000 m od zámku, čili 8 km.
Výsledek: 8000 m
Hint: Určete vzájemnou rychlost, tedy jakým tempem se Cipísek přibližuje vzhledem k Rumcajsovi.
ID: 9;
Tags: vzájemná rychlost;
Autor: Marek Scholz (admin);
Position: /9;
▮
Zrychlení formule 1
#10,
Marek Scholz (admin),
pos:1/9,
kat
Formule F1 zrychlí z 0 na 100 km/h zhruba za 2,5 sekundy. Jaké je její průměrné zrychlení? Pozor na jednotky. Výsledek uveďte jako celé číslo v jednotce m/s2. K diskuzi - porovnejte zrychlení formule s gravitačním zrychlením a také se zrychlením obyčejného osobního auta.
Řešení: Nejprve převedeme rychlost z km/h na m/s:
$v = 100 \, \text{km/h} = 100 : 3,6 \, \text{m/s} = 27,78 \, \text{m/s}$.
Formule se rozjíždí z klidu a její změna rychlosti je tedy právě $\Delta v = 27,78\,\text{m/s}$.
Průměrné zrychlení $a$ je dáno vztahem:
$a = \frac{\Delta v}{\Delta t} = \frac{27,78 \, \text{m/s}}{2,5 \, \text{s}} = 11,11 \, \text{m/s}^2$.
Všimněme si, že to je více než gravitační zrychlení. Pokud bychom s běžným autem chtěli tolik zrychlit, zahrabaly by kola. K takovémuto zrychlení jsou potřeba speciální pneumatiky, snížené těžiště, zvýšený přítlak atp. Běžné auta zrychlí z 0 na 100 km/h za zhruba 7 sekund, zrychlení je tak oproti formuli 2-4 krát menší.
Výsledek: 11 m/s2
Hint: Nezapomeňte převést km/h na m/s!
ID: 10;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Síla na auto
#71,
Marek Scholz (admin),
pos:1/9,
kat
Na obrázku jsou zachyceny polohy auta vždy po půl sekundě. Rozhodněte, zda na auto působí nenulová výsledná síla, a pokud ano, tak určete její směr.

obr.
skrýt |
S |
M |
L
Řešení: Rozestupy jsou stejné, tedy auto má stále stejnou rychlost a jede rovnoměrně. Proto výsledná síla je nulová.
Výsledek: je nulová
ID: 71;
Tags: zákon setrvačnosti;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Otázečky na zákon síly
#70,
Marek Scholz (admin),
pos:3/9,
kat
Pár jednoduchých otázeček:
a) Bylo zjištěno, že na Měsíci na závaží o hmotnosti 500 g působí gravitační síla o velikosti 0,8 N. S jakým zrychlením bude závaží padat k povrchu Měsíce?
b) Malý výtah o hmotnosti 400 kg se rozjíždí vzhůru se zrychlením 1,5 m/s2. Jakou velikost má výsledná síla, která na výtah působí? *Jakou velikost má síla, kterou za výtah táhne lano, na kterém je výtah pověšený?
c) Na vozíček působila brzdná síla o velikosti 200 N, přičemž vozík začal zpomalovat se zrychlením 4 m/s2. Jaká je hmotnost vozíku?
d) Fotbalový míč o hmotnosti 400 g padá přímo dolů a působí na něj odpor vzduchu o velikosti 1,6 N. Jakou velikost má zrychlení míče?
e) Pan Jouda roztlačuje dokonale promazaný vozík o hmotnosti 250 kg silou o velikosti 200 N. Za jak dlouho vozík dosáhne rychlosti běhu, čili rychlosti 4 m/s?
Řešení: a) Víme $a = F/m = 0,8\,\mathrm{N} /0,5\,\mathrm{kg} = 1,6\,\mathrm{m/s^2}$. To je vlastně hodnota gravitačního zrychlení na Měsíci.
b) Platí $F_v = ma = 400 \cdot 1,5 = 600\,\mathrm{N}$. To je hodnota výsledné síly. Na výtah ale působí gravitační síla 4000 N. Síla od lana proto musí být 4600 N, aby výslednice byla právě 600 N.
c) Víme $a = F/m$ a proto $m = F/a = 200 / 4 = 50\,\mathrm{kg}$.
d) Na míč působí gravitační síla $F_g = mg = 4\,\mathrm{N}$ směrem dolů. Odporová síla 1,6 N působí při pádu směrem nahoru. Výsledná síla na míč je 4-1,6 = 2,4 N. Zrychlení míče je $a = F_v/m = 2,4/0,4 = 6\,\mathrm{m/s^2}$.
e) Víme $a = F/m = 200\,\mathrm{N}/250\,\mathrm{kg} = 0,8\,\mathrm{m/s^2}$. Změna rychlosti je o 4 m/s, tedy bude trvat $t = \Delta v/a = 4/0,8 = 5\,\mathrm{s}$.
Výsledek: a) 1,6 m/s2; b) výslednice 600 N, od lana 4600 N; c) 50 kg; d) 6 m/s2; e) 5 s
ID: 70;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Výslednice na auto
#72,
Marek Scholz (admin),
pos:1/9,
kat
Na obrázku jsou zachyceny polohy auta vždy po půl sekundě. Rozhodněte, zda na auto působí nenulová výsledná síla, a pokud ano, tak určete její směr.

obr.
skrýt |
S |
M |
L
Řešení: Auto brzdí, tedy má zrychlení proti směru pohybu. Výslednice je nenulový a míří proti pohybu - doleva.
Výsledek: nenulová doleva
ID: 72;
Tags: zákon setrvačnosti;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Kulička ve vlaku
#75,
Marek Scholz (admin),
pos:1/9,
kat
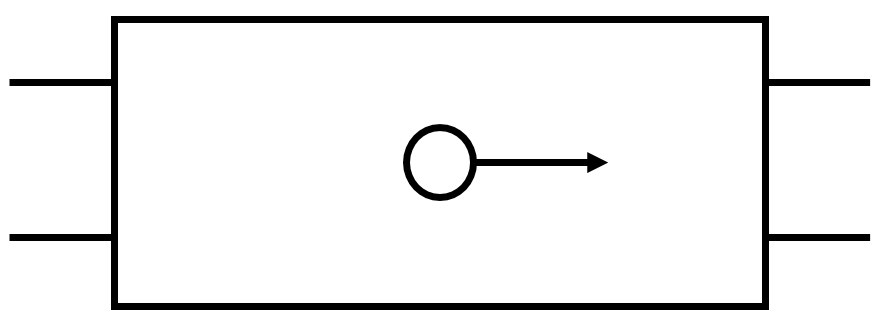
Kulička leží ve vagonu na vodorovné podlaze a kromě síly svislé síly gravitační a síly od podložky na ni nepůsobí žádná další síla. V určité chvíli se kulička začne pohybovat vyznačeným směrem. Určete co nejpřesněji, co se může dít s vlakem (dvě různé situace).
obr.
skrýt |
S |
M |
L
Řešení: 1) Vlak jede směrem doprava a začne brzdit. Kulička má tendenci setrvávat v pohybu.
2) Vlak se rozjíždí (zrychluje) směrem doleva. Kulička má tendenci setrvávat v klidu.
Výsledek: 1) Vlak jede směrem doprava a začne brzdit. 2) Vlak se rozjíždí (zrychluje) směrem doleva.
ID: 75;
Tags: zákon setrvačnosti;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Kulička ve vlaku
#76,
Marek Scholz (admin),
pos:1/9,
kat
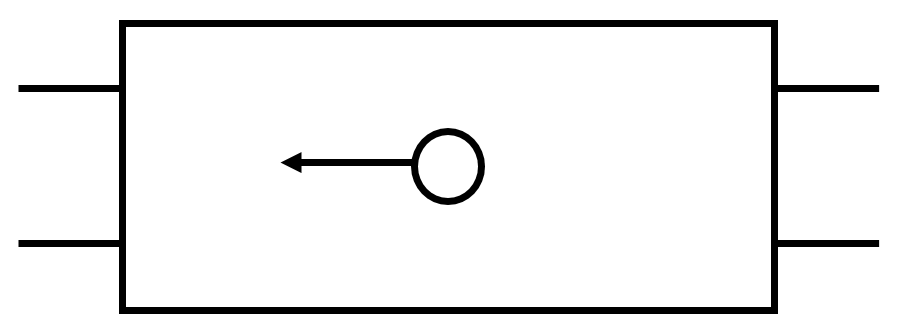
Kulička leží ve vagonu na vodorovné podlaze a kromě síly svislé síly gravitační a síly od podložky na ni nepůsobí žádná další síla. V určité chvíli se kulička začne pohybovat vyznačeným směrem. Určete co nejpřesněji, co se může dít s vlakem (dvě různé situace).
obr.
skrýt |
S |
M |
L
Řešení: 1) Vlak jede směrem doleva a začne brzdit. Kulička má tendenci setrvávat v pohybu.
2) Vlak se rozjíždí (zrychluje) směrem doprava. Kulička má tendenci setrvávat v klidu.
Výsledek: 1) Vlak jede směrem doleva a začne brzdit. 2) Vlak se rozjíždí (zrychluje) směrem doprava.
ID: 76;
Tags: zákon setravčnosti;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Závaží na pružině ve výtahu
#77,
Marek Scholz (admin),
pos:1/9,
kat
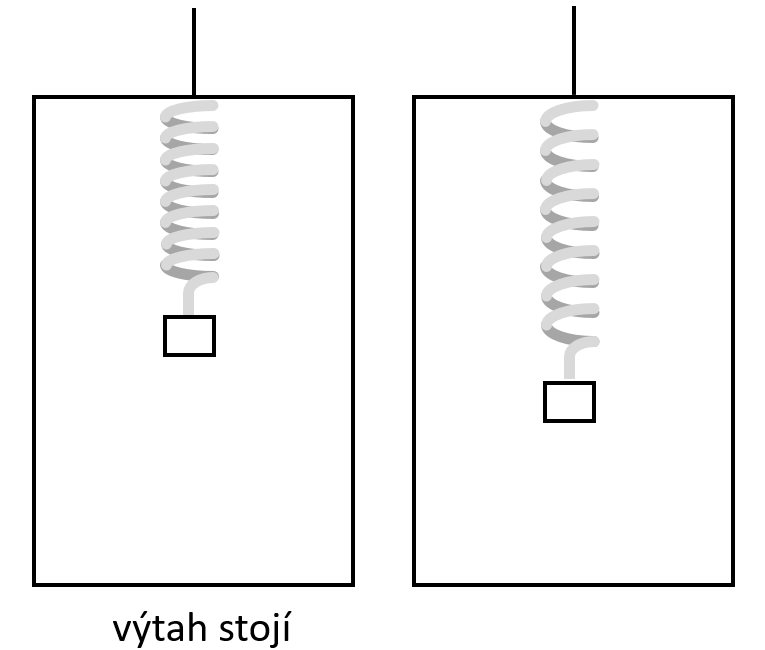
Ve výtahu je závaží zavěšené na pružině. Když je výtah v klidu, tak pružina vypadá jako na obrázku vlevo. Kydž se však výtah nějakým způsobem pohybuje, tak se pružina ustálí v poloze jako na obrázku v pravo. Jakými způsoby by se výtah mohl pohybovat, aby toto nastalo?
obr.
skrýt |
S |
M |
L
Řešení: 1) Výtah se rozjíždí (zrychluje) směrem nahoru. Kulička má tendenci setrvat v klidu (či v původní rychlosti), proto se pružina více protáhne.
2) Výtah jede směrem dolů a brzdí. Kulička má tendenci setrvávat v původním pohybu (rychlosti) směrem dolů, proto se pružina vác protáhne.
Výsledek: 1) Výtah se rozjíždí (zrychluje) směrem nahoru. 2) Výtah jede směrem dolů a brzdí.
ID: 77;
Tags: zákon setrvačnosti;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Součinitel tření
#57,
Marek Scholz (admin),
pos:1/9,
kat
Seřaďte následující dvojice povrchů podle toho, které přísluší největší a které nejmenší součinitel smykového tření: kartonová krabice - lino; pneumatika - silnice; kolo vlaku - kolejnice. Vyberte, která má největší součinitel.
Řešení:
Výsledek: pneumatika - silnice
ID: 57;
Tags: smykové tření;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Tlačení krabice
#59,
Marek Scholz (admin),
pos:1/9,
kat
Helmut tlačí po podlaze dřevěnou krabici o hmotnosti 15 kg. Jakou silou musí vodorovně působit, aby krabici udržoval v rovnoměrném pohybu? Koeficient tření krabice-podlaha budiž 0,3. Uvažujte g = 10 m/s2.
Řešení: $F_t = F_n \cdot f = mgf = 150\,\mathrm{N} \cdot 0,3 = 45\,\mathrm{N}$.
Výsledek: 45 N
ID: 59;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Součinitel tření
#61,
Marek Scholz (admin),
pos:1/9,
kat
Anežka ví, že k tažení kvádříku o hmotnosti 200 g po vodorovné desce stolu potřebovala působit silou o velikosti 0,7 N. Určete součinitel smykového tření mezi stolem a kvádříkem.
Řešení: $F_t = F_n \cdot f = mgf$, tedy $f = F_t/mg = 0,7\,\mathrm{N} / 2 \,\mathrm{N} = 0,35$.
Výsledek: 0,35 N
ID: 61;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Přetržený provázek
#62,
Marek Scholz (admin),
pos:2/9,
kat
Helmut si znovu vzal kartonovou krabici, ale tentokrát ji zapřáhnul za provázek a začal tahat po koberci, kde je koeficient smykového tření roven 0,4. Helmut ví, že když by na provázek zavěšoval závaží, tak vydrží zatížení max. 10 kg. Jakou maximální hmotnost může mít krabice, aby ji ještě mohl na provázku rovnoměrně táhnout?
Řešení: Maximální síla napnutí provázku je F = 100 N. Pro rovnoměrné tažení je potřeba síla $F = mgf$. Odtud $m = F/gf = 100\,\mathrm{N} / (10\,\mathrm{m/s^2} \cdot 0,4) = 25\,\mathrm{kg}$.
Výsledek: 25 kg
Hint: Ze zadání je patrné, že pokud bude třecí síla větší než 100 N, tak už ji Helmut nebude schopen na provázku táhnout.
ID: 62;
Tags: ;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Tlačit proti stěně
#63,
Marek Scholz (admin),
pos:2/9,
kat
Když nesete těžkou krabici (třeba 16 kg), můžete si ulevit tím, že ji na chvíli zatlačíte proti stěně. Jakou silou je potřeba tlačit proti stěně, aby krabice nesklouzla? Budiž f = 0,65. Nakreslete také všechny síly působící na krabici. Uvažujte g = 10 m/s2.
Řešení: Přítlačnou sílu kolmo ke stěně označme $F_n$. Třecí síla musí vyrovnat tíhovou sílu, tedy má být $F_t = 160\,\mathrm{N} = fF_n$, tedy $F_n = 160\,\mathrm{N} / f = 246\,\mathrm{N}$.
Výsledek: 246 N
ID: 63;
Tags: ;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Puk na ledě
#78,
Marek Scholz (admin),
pos:3/9,
kat
Puk klouže po nekvalitním ledu, přičemž koeficient smykového tření mezi pukem a ledem je f = 0,1. Jaká je velikost zrychlení (čili zpomalení) puku?
Řešení: $F_t = F_n \cdot f = mgf$.
Zpomalení v důsledku tření je
$a = F_t/m = mgf/m = gf = 9,8 \cdot 0,1 = 0,98\,\mathrm{m/s^2}$.
Vidíme, že pro velikost zrychlení stačí přenásobit gravitační zrychlení koeficientem tření.
Výsledek: 0,98 m/s2
ID: 78;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Dvě různé podlahy
#239,
Marek Scholz (admin),
pos:1/9,
kat
Pan Vrták rovnoměrně táhne bednu o hmotnosti 20 kg po podlaze a potřebuje k tomu tažnou sílu 50 N. Poté táhne bednu o hmotnosti 30 kg po jiné podlaze a potřebuje k tomu sílu 60 N. Ve kterém případě je "míra drhnutí povrchů" větší? Zdůvodněte a doprovoďte výpočtem.
ID: 239;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Rozhodni o rovině
#73,
Marek Scholz (admin),
pos:/9,
kat
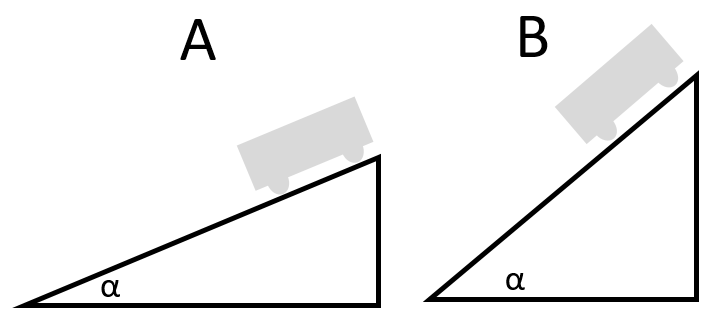
Ve kterém z případů bude na vozík na rampě působit větší síla ve směru pohybu a a tedy vozík bude mít větší zrychlení?
obr.
skrýt |
S |
M |
L
Řešení: B - prudší svah, větší zrychlení.
Výsledek: B
ID: 73;
Tags: nakloněná rovina;
Autor: Marek Scholz (admin);
Position: /9;
▮
Rozhodni o přítlačné síle
#74,
Marek Scholz (admin),
pos:/9,
kat
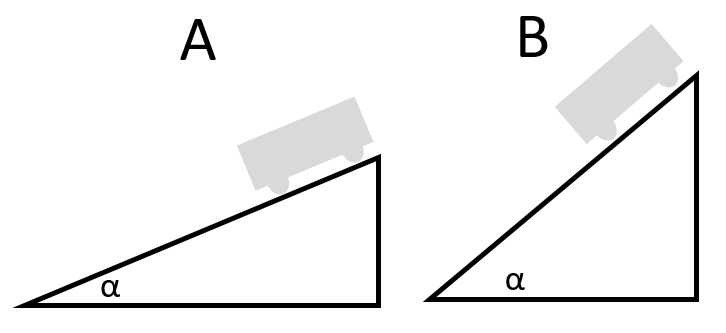
Ve kterém z případů bude vozík na rampě více tlačit do kolejí?
obr.
skrýt |
S |
M |
L
Řešení: Menší úhel sklonu, větší síla kolmo do podložky.
Výsledek: A
ID: 74;
Tags: nakloněná rovina, normálová síla;
Autor: Marek Scholz (admin);
Position: /9;
▮
Střela do zloděje
#23,
Marek Scholz (admin),
pos:4/9,
kat
Zloděj zmrzliny o hmotnosti 80 kg stojí na kluzkém ledě a uvízne v něm střela, která letěla rychlostí 800 m/s a měla hmotnost 3 g. Jakou rychlostí se po ledě rozpohybuje zločinec?
Řešení: Zákon zachování hybnosti pro tento případ říká:
$m_{\text{zločinec}} \cdot v_{\text{zločinec}} + m_{\text{střela}} \cdot v_{\text{střela}} = (m_{\text{zločinec}} + m_{\text{střela}}) \cdot v_{\text{konečná}}$
Protože zločinec na začátku stojí, jeho počáteční rychlost $v_{\text{zločinec}} = 0$. Rovnice se zjednoduší na:
$m_{\text{střela}} \cdot v_{\text{střela}} = (m_{\text{zločinec}} + m_{\text{střela}}) \cdot v_{\text{konečná}}$
Vyjádříme konečnou rychlost $v_{\text{konečná}}$:
$v_{\text{konečná}} = \frac{m_{\text{střela}} \cdot v_{\text{střela}}}{m_{\text{zločinec}} + m_{\text{střela}}}$
Dosadíme hodnoty:
$v_{\text{konečná}} = \frac{0{,}003 \cdot 800}{70 + 0{,}003} \approx 0{,}034 \, \text{m/s}$
Výsledek: 3 cm/s
Hint: Hybnost celého systému na začátku i na konci musí být stejná.
ID: 23;
Tags: ;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Hybnost auta a dodávky
#82,
Marek Scholz (admin),
pos:1/9,
kat
Dodávka o hmotnosti 3,5 tuny jede rychlostí 60 km/h. Jakou rychlost by muselo mít osobní auto o hmotnosti 1,5 tuny, aby mělo stejnou hybnost jako dodávka?
Určete v km/h.
Řešení: Má platit $m_1v_1 = m_2v_2$, neboli
$3,5 \cdot 60 = 1,5 \cdot v$,
tedy $v = 60\,\mathrm{km/h} \cdot 3,5/1,5 = 140\,\mathrm{km/h}$.
Kolikrát menší je hmotnost, tolikrát větší musí mít rychlost.
Všimněme si, že jsme km/h nepřeváděli na m/s. Zde si to můžeme dovolit, musíme ale mít na paměti, že když jsme rychlost dodávky vyjádřili v km/h, tak výsledná rychlost auta taky vyjde v km/h. Pokud nepřevedeme na základní jednotky, tak vždy musíme vědět, proč tak činíme.
Výsledek: 140 km/h
ID: 82;
Tags: hybnost;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Strčení do bruslaře
#83,
Marek Scholz (admin),
pos:2/9,
kat
O kolik se změní rychlost bruslaře o hmotnosti 50 kg, když do něj někdo tlačí silou o velikosti 40 N po dobu půl sekundy? Bruslař bez tření klouže po ledě. K výpočtu použijte vztah pro impuls síly.
Řešení: Zápis: $m$ = 50 kg; $F$ = 40 N; $\Delta t$ = 0,5 s; $\Delta v$ = ?;
Impuls síly:
$\Delta p = F \cdot \Delta t$,
čili
$m \Delta v = F \cdot \Delta t$
obě strany rovnice vydělíme $m$:
$\Delta v = F \cdot \Delta t / m$
$\Delta v$ = 40 N $\cdot$ 0,5 s / 50 kg = 0,4 m/s.
Můžeme samozřejmě řešit i bez impulsu síly, prostě na základě druhého Newtonova zákona $a = F/m$. Zkuste si.
Výsledek: 0,4 m/s
Hint: Impuls síly: $\Delta p = F \cdot \Delta t$.
ID: 83;
Tags: hybnost, impuls síly;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Hybnost auta a náklaďáku
#81,
Marek Scholz (admin),
pos:1/9,
kat
Osobní auto o hmotnosti 1,5 tuny jede rychlostí 30 m/s (čili 108 km/h). Jakou rychlostí by muselo jet nákladní auto o hmotnosti 7,5 tuny, aby mělo stejnou hybnost?
Řešení: Zápis: $m_1$ = 1500 kg; $v_1$ = 30 m/s; $m_2$ = 7500 kg; $v_2$ = ?
Má platit $p_1 = p_2$, neboli
$m_1v_1 = m_2v_2$.*
Nyní mohu provést úvahu, že náklaďák má 5x větší hmotnost, a tedy musí mít 5x menší rychlost, neboli 6 m/s.
Nebo mohu dosadit do vztahu * výše:
$1500\,\mathrm{kg} \cdot 30\,\mathrm{ms^{-1}} = 7500\,\mathrm{kg} \cdot v_2$.
$v_2 = 30 \cdot 1500/7500 = 6\,\mathrm{m/s}$.
Ze vztahu * mohu samozřejmě také vyjádřit $v_2$ obecně
$\frac{m_1}{m_2}v_1 = v_2$ a pak až dosadit.
Výsledek: 6 m/s
Hint: Musí platit $m_1v_1 = m_2v_2$.
ID: 81;
Tags: hybnost;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Katapult na kolečkách
#87,
Marek Scholz (admin),
pos:3/9,
kat
Katapult na kolečkách má hmotnost 200 kg. Při válce gangů vystřelil vodorovným směrem medicimbal o hmotnosti 8 kg rychlostí 50 m/s vůči zemi. Jakou rychlostí ze rozpohybuje katapult v opačném směru (tedy jaká je rychlost zpětného rázu)?
Řešení: Katapult a medicimbál na sebe působí vzájemně stejně velkými silami opačného směru a tedy během výstřelu získají stejně velké hybnosti opačného směru. Hybnost medicimbálu vůči zemi je
$m_m v_m$ = 400 kg.m/s.
Mohu si jednoduše říct, žatapult má 25x větší hmotnost a jeho rychlost tak bude 25x menší, čili 2 m/s.
Nebo si mohu říci, že hybnost katapultu musí být taktéž 400 kg.m/s, a tedy jeho rychlost musí být
$v_k = p_k/m_k = 400 / 200 = 2\,\mathrm{m/s}$.
Výsledek: 2 m/s
ID: 87;
Tags: zpětný ráz;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Indiana Jones naskakuje
#123,
Marek Scholz (admin),
pos:4/9,
kat
Indiana Jones vypasený na hmotnost 80 kg běží rychlostí 10 m/s podle kolejí úzkokolejky. Před ním stojí nehybný prázdný důlní vozík o hmotnosti 240 kg. Indianovi se vylíhl v hlavě nápad, že do vozíku naskočí. Jaká bude výsledná rychlost vozíku spolu s Indianou, poté co naskočil?
Řešení: Zápis: $m_1$ = 80 kg; $v_1$ = 10 m/s; $m_2$ = 240 kg; $v_2$ = 0 m/s;
Výsledná hmotnost $m = m_1 + m_2$. Chceme spočítat výslednou rychlost $v$.
Celková hybnost Indiany a vozíku na začátku musí být stejná jako jejich celková hybnost na konci. Odtud rovnice:
$p_1 + p_2 = p$
$m_1v_1 + m_2v_2 = (m_1 + m_2)v$,
čili
$(80\,\mathrm{kg}\cdot 10\,\mathrm{m/s}) + 0 = 320\,\mathrm{kg}\cdot v$
tedy
$v = v_1m_1/(m_1+m_2) = (80\,\mathrm{kg}\cdot 10\,\mathrm{m/s}) / 320\,\mathrm{kg} = 2,5\,\mathrm{m/s}$
Výsledná rychlost je tedy 4x menší než počáteční rychlost Indiany.
Na to jsme mohli ale přijít rovnou: Indiana jakoby ztěžkl o hmotnost celého vozíku, takže nová hmotnost je 4x větší než ta původní, ale hybnosti mají být zachovány, tedy výsledná rychlost musí být 4x menší.
Výsledek: 2,5 m/s
Hint: Celková hybnost Indiany a vozíku na začátku musí být stejná jako jejich celková hybnost na konci.
ID: 123;
Tags: ;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Auto v zatáčce
#287,
Marek Scholz (admin),
pos:5/9,
kat
Auto projíždí zatáčkou. Aby nedostalo smyk, musí ho v zatáčce držet třecí síla mezi pneumatikami a silnicí. Kolikrát se zvýší síla mezi pneumatikami a silnicí, když auto projede zatáčkou rychlostí 70 km/h namísto 50 km/h?
Řešení:
Výsledek: 1,96 -krát
ID: 287;
Tags: ;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Kulička na niti
#288,
Marek Scholz (admin),
pos:5/9,
kat
Helmut přidělal železnou kuličku na nit a začal s ní točit nad hlavou. Kulička má hmotnost 200 g a na niti se pohybuje po kružnici s poloměrem 80 cm. Helmut ví, že nit vydrží působit silou maximálně 10 N a při větší síle se přetrhne. Jakou maximální obvodovou rychlostí se může kulička pohybovat, aniž by se nit přetrhla? (* za jak dlouho pak kulička proběhne jednu otočku?)
Řešení:
Výsledek: 6,32 m/s
ID: 288;
Tags: ;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Vesmírný válec
#289,
Marek Scholz (admin),
pos:5/9,
kat
Vesmírná loď má tvar válce, který rotuje kolem své osy. Tím je v lodi zajištěna umělá gravitace. Lidé mohou chodit po vnitřním plášti válce a cítí gravitační zrychlení o stejné velikosti, jako je tomu na zemi. Povrch válce se pohybuje obvodovou rychlostí 50 m/s. Jaký poloměr má válec?
ID: 289;
Tags: ;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Tvrzení o dostředivé síle a zrychlení
#290,
Marek Scholz (admin),
pos:5/9,
kat
Vyberte všechna pravdivá tvrzení:
a) Když projedeme zatáčku dvojnásobnou rychlostí, tak na mě musí sedačka působit dvojnásobně velkou dostředivou silou.
b) Když je zatáčka prudší, tak to znamená, že má menší poloměr.
c) Velikost dostředivého zrychlení auta v zatáčce nezávisí na jeho hmotnosti, ale velikost dostředivé síly ano.
d) Okamžitá rychlost auta projíždějícího zatáčkou má směr do středu zatáčky.
Odpověď pisšte ve formě abcd
ID: 290;
Tags: ;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Práce při zvedání kýble
#147,
Marek Scholz (admin),
pos:1/9,
kat
Jak velkou práci vykonám, když rovnoměrně zvednu kýbl s vodou o hmotnosti 5 kg do výšky 60 cm?
Uvažujte g = 10 m/s2
Řešení: $W = F \cdot s = 50\,\mathrm{N} \cdot 0,6\,\mathrm{m} = 30\,\mathrm{J}$.
Výsledek: 30 J
Hint: Nezapomeňte převést na základní jednotku.
ID: 147;
Tags: práce,t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Tři síly na vozík
#149,
Marek Scholz (admin),
pos:1/9,
kat
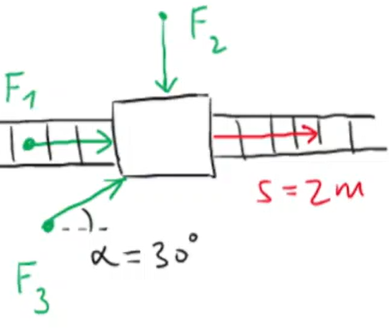
Na kolejích stojí těžký vozík. Ciri, Geralt a Yennefer na vozík působí silami F1, F2 a F3 a tlačí ho po kolejích. Velikosti sil jsou shodné. Kdo z nich koná nulovou užitečnou práci?
obr.
skrýt |
S |
M |
L
Řešení:
Výsledek: Nulovou práci koná Geralt (F2), působí kolmo na posunutí.
ID: 149;
Tags: práce, rozklad sil, t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Práce při tlačení bedny
#148,
Marek Scholz (admin),
pos:1/9,
kat
Pan Šňup obdržel velkou a těžkou krabici s banány, o hmotnosti 20 kg. Potřebuje ji po podlaze přesunout na druhou stranu místonosti do vzdálenosti 8 m. Koeficient tření mezi podlahou a krabicí je roven 0,3. Určete velikost práce, kterou pan Šňup musí vykonat.
Řešení: Síla pana Šňupa musí překonávat třecí sílu, pro rovnoměrné tlačení krabice tak potřebuje vyvinout sílu právě rovnou třecí síle.
Velikost smykové třecí síly je
$F_t = f \cdot F_n = fmg = 0,3 \cdot 200\,\mathrm{N} = 60\,\mathrm{N}$
$W = F \cdot s = F_t \cdot s = 60\,\mathrm{N} \cdot 8\,\mathrm{m} = 480\,\mathrm{J}$
Vykoná práci 480 J.
Výsledek: 480 J
Hint: Pan Šňup musí působit silou stejně velkou, jako je smyková třecí síla.
ID: 148;
Tags: práce, t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Práce s pytlem cementu
#151,
Marek Scholz (admin),
pos:1/9,
kat
Helmut staví dům. Pomocí jednoduché kladky a lana zvedá pytel cementu o hmotnosti 15 kg z původní výšky 3 m do finální výšky 10 metrů. Jak velkou práci při tom vykoná?
Řešení: Stačí si jen uvědomit, že pytel se posune o 7 metrů. Potom
$W = F \cdot s = 150\,\mathrm{N} \cdot 7\,\mathrm{m} = 1050\,\mathrm{J}.
Výsledek: 1050 J
ID: 151;
Tags: práce, t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Kinetická energie při pádu
#181,
Marek Scholz (admin),
pos:3/9,
kat
Zkušený skokan Helmut skáče do vody z výšky 40 m. Jakou velikost bude mít jeho kinetická energie dvě sekundy po seskoku? Helmut nechť má hmotnost 70 kg. Odpor vzduchu zanedbejte a pokud použijete nějaký fyzikální parametr, užijte co nejpřesnější hodnotu.
Řešení: Dvě sekundy po seskoku bude mít rychlost $v = 2g$ = 19,62 m/s.
Z toho plyne kinetická energie
$E_k = \frac{1}{2}mv^2$ = $\frac{1}{2} \cdot 70\,\mathrm{kg} \cdot (30\,\mathrm{m/s})^2$ = 13473 J.
Výsledek: 13473 J
ID: 181;
Tags: kinetická energie, t-kineticka-energie;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Kinetická energie míče
#185,
Marek Scholz (admin),
pos:3/9,
kat
Jakou rychlostí byste museli vykopnout fotbalový míč, aby jeho kinetická energie byla 1 kJ? Je to realistické?
Pro číselný výpočet uvažujte hmotnost fotbalového míče 420 g.
Řešení: $E_k = \frac{1}{2}mv^2$
Vyjádříme $v$:
$v = \sqrt{2E_k/m}$ $= \sqrt{2000\,\mathrm{J} / 0.42\,\mathrm{kg}} = 69\,\mathrm{m/s}$.
To je 248 km/h a je to již pravděpodobně nad běžné lidské možnosti.
Výsledek: 69 m/s
ID: 185;
Tags: kinetická energie, pohybová energie, t-kineticka-energie;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Elektrárna na potenciální energii
#208,
Marek Scholz (admin),
pos:4/9,
kat
Víte, ve kterém typy elektráren se využívá přeměny tíhové potenciální energie na kinetickou energii a nakonec na elektrickou energii. Popište, jak se v elektrárně tyto energie v sebe proměňují.
Řešení: Vodní elektrárna či přečerpávací elektrárna. Voda klesá a ztrácí potenciální energii, přitom roztáčí turbínu (kinetická energie). Turbína roztáčí generátor střídavého proudu. To už je ale jiný příběh.
Výsledek:
ID: 208;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Pád ze třetího patra
#194,
Marek Scholz (admin),
pos:5/9,
kat
Ve filmu Copak je to za vojáka skáče vojín Kouba ze třetího patra, aby se včas dostal na nástup jednotky. Pokud by tak učinil, jaká bude jeho rychlost při dopadu na zem? Řešte na základě zákona zachování mechanické energie.
Pro výpočet uvažujte, že skáče z výšky 7 metrů. $g = 9,81\,\mathrm{m/s^2}$.
Řešení: Při skoku ze třetího patra máme dvě patra pod sebou. Výška patra bývá okolo 3 m a při skoku z okna tak lze odhadnout, že výška nad zemí je třeba 7 metrů.
Zákon zachování energie říká, že součet potenciální a kinetické na začátku i na konci bude stejný:
$E_{p1} + E_{k1} = E_{p2} + E_{k2}$
Počáteční kinetická energie je nulová, stejně tak jako koncová potenciální energie. Tedy:
$E_{p1} + 0 = 0 + E_{k2}$
Čili vztah se redukuje na
$mgh = \frac{1}{2}mv^2$,
což odpovídá tomu, že se Veškerá potenciální energie přemění na kinetickou energii. Neznámá je rychlost $v$, kterou chceme ze vztahu osamostatnit.
V první řadě si všimneme, že na obou stranách můžeme vykrátit hmotnost a dostaneme
$gh = \frac{1}{2}v^2$
Obě strany násobíme dvěma a máme
$2gh = v^2$
čili
$v = \sqrt{2gh}$ $= \sqrt{2 \cdot 9,8\,\mathrm{m/s^2} \cdot 7\,\mathrm{m}}$ = 11,7 m/s = 42,2 km/h.
Je to hodně nebo málo? Zkuste někdy jít pomalou chůzí rychlostí 2 km/h a jen tak narazit do stěny. Uvidíte, jak se potlučete...
Výsledek: 11,7 m/s
ID: 194;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Práce s půllitrem
#207,
Marek Scholz (admin),
pos:2/9,
kat
Ze stolu o výšce 70 cm zvedáte půllitr s limonádou o hmotnosti 800 g. Určete, do jaké výšky nad zemí byste museli zvednout půllitr, abyste vykonali práci o velikosti 6 J? Uvažujte g = 10 m/s2.
Uveďte v centimetrech.
Řešení: Práce při zvedání tělesa proti gravitaci se rovná přírůstku potenciální energie:
$W = m g (h - h_0)$
Kde:
- $W = 6\ \text{J}$
- $m = 0{,}8\ \text{kg}$
- $g = 10\ \text{m/s}^2$
- $h_0 = 0{,}70\ \text{m}$ (výška stolu)
- $h$ = hledaná výška nad zemí
Dosadíme:
$6 = 0{,}8 \cdot 10 \cdot (h - 0{,}70)$
$6 = 8(h - 0{,}70)$
$\frac{6}{8} = h - 0{,}70$
$0{,}75 = h - 0{,}70$
$h = 0{,}75 + 0{,}70 = 1{,}45\ \text{m}$
Půllitr musíte zvednout do výšky 1,45 metru nad zemí.
Výsledek: 145 cm
ID: 207;
Tags: potenciální energie, t-potencialni-energie;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Helmut kope na Marsu
#213,
Marek Scholz (admin),
pos:5/9,
kat
Helmut byl na dovolené na Měsící. Vystřelil vzhůru tenisový míček rychlostí 40 m/s. Určete, do jaké výšky vystoupá, použijte zákon zachování energie.
Řešení: Zákon zachování energie:
$\frac{1}{2} m v_1^2 + m g' h_1 = \frac{1}{2} m v_2^2 + m g' h_2$
se zjednoduší, protože je počáteční výška nulová a koncová rychlost je nulová, čili
$\frac{1}{2} m v_1^2 = m g h_2$
Buď rovnou dosadíme a potom vyjádříme $h_2$, nebo vyjádříme ještě "s písmenky".
Samozřejmě po cestě krátíme $m$:
$h_2 = v_1^2/2g$
Dosadíme v základních jednotkách, přičemž gravitační zrychlení na Měsící je $g = 1,62\,\mathrm{m/s^2}$:
$h_2 = 40^2/3,24 = 494\,\mathrm{m}$.
Vystoupá do výšky 494 metrů! To je překvapivě hodně vysoko.
Výsledek: 494 m
ID: 213;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Účinnost rychlovarné konvice
#221,
Marek Scholz (admin),
pos:6/9,
kat
Rychlovarná konvice má příkon 1600 W. Ohřívání vody na čaj trvalo 4 minuty a konvice vodě dodala teplo o velikosti 300 kJ. Určete účinnost ohřevu vody v konvici.
Řešení: $P_0 = 1600\,\mathrm{W}$; $t = 4\,\mathrm{min} = 240\,\mathrm{s}$; $W = 300\,\mathrm{kJ}$.
$\eta = W/E = W/(P_0 t)$ = 300000 J / (1600 W * 240 s) = 0,78 = 78%.
Výsledek: 78 %
ID: 221;
Tags: výkon, účinnost, t-vykon;
Autor: Marek Scholz (admin);
Position: 6/9;
▮
Výkon elektromotoru
#222,
Marek Scholz (admin),
pos:6/9,
kat
Výkon elektrického motoru je 2,4 kW a jeho účinnost je 75%. Určete příkon motoru.
Řešení: $\eta = P/P_0$, čili $P_0 = P/\eta$ = 2,4 kW / 0,75 = 3,2 kW.
Výsledek: 3,2 kW
ID: 222;
Tags: výkon, účinnost, t-vykon;
Autor: Marek Scholz (admin);
Position: 6/9;
▮
Kilowatt po celou hodinu
#224,
Marek Scholz (admin),
pos:6/9,
kat
Elektrické topení má příkon 1 kW a běží po dobu jedné hodiny. Jaké množství elektrické energie spotřebuje? Určete v megajoulech.
Řešení: $E = P_0 t$ = 1000 W * 3600 s = 3 600 000 J = 3,6 MJ.
Zároveň ale spotřebovanou energii mohu vyjádřit jako 1 kW * 1 h = 1 kWh.
Tedy topení spotřebuje energii o velikosti 1 kilowatthodina = 3,6 MJ.
Výsledek: 3,6 MJ
ID: 224;
Tags: výkon, t-vykon;
Autor: Marek Scholz (admin);
Position: 6/9;
▮
Potenciální energie paní Mrtvé
#217,
Marek Scholz (admin),
pos:2/9,
kat
Paní Mrtvá stojí na zemi v pátém patře (páté nadzemní podlaží), ve výšce 13 m nad silnicí. Určete velikost její potenciální energie vůči
a) silnici
b) vůči panu Živnému, který bydlí ve druhém patře.
c) vůči podlaze bytu paní Mrtvé.
d) vůči stropu jejího bytu
e) vůči paní Zkyslé, která bydlí o patro výš.
Všechny potřebné vzdálenosti, výšky a další údaje rozumně odhadněte.
Řešení: Budiž hmotnost paní Mrtvé 60 kg. Potenciální energii vždy určíme ze vztahu $E_p = mgh$.
Vždy ale musíme určit, vůči čemu odměřujeme výšku.
Paní Mrtvá má těžiště zhruba 1 m nad podlahou. Odtud odvodíme, že výška patra jsou zhruba 3 metry.
a) vůči silnici - 60 x 10 x 13 = 7800 J
b) vůči panu Živnému, který bydlí ve druhém patře - dělí je 3 patra, výškový rozdíl je 9 metrů, čili 60 x 10 x 9 = 5400 J.
c) vůči podlaze bytu paní Mrtvé - těžiště jeden metr nad podlahou, čili 600 J.
d) vůči stropu jejího bytu - paní Mrtvá je pod stropem ve výšce asi 2 metry. Světe div se, její potenciální energie vůči stropu bude záporná v hodnotě -1200 J
e) vůči paní Zkyslé, která bydlí o patro výš - výška patra 3 metry, čili potenciální energie paní Mrtvé je -1800 J.
Výsledek:
ID: 217;
Tags: potenciální energie, t-potencialni-energie;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Odrazy tenisového míčku
#230,
Marek Scholz (admin),
pos:4/9,
kat
Imhotep zvedl tenisový míček a pustil ho na podlahu. Míček na podlaze skákal, ale po každém odrazu vyskočil trochu méně. Popište podrobně všechny přeměny energie, ke kterým docházelo od okamžiku vypuštění míčku až do okamžiku kdy míček po odrazu zase vystoupal do nejvyššího bodu.
ID: 230;
Tags: t-ZZME, zákon zachování mechanické energie;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Výkon motoru
#231,
Marek Scholz (admin),
pos:7/9,
kat
Motor auto pohání silou 400 N, přičemž auto ujede během pěti minut 6 kilometrů. Určete výkon motoru.
Řešení: Zápis: F = 400 N; t = 5 min = 300 s; s = 6 km = 6000 m.
Pro výkon platí:
$P = W/t = Fs/t$ = (400 N * 6000 m) / 300 s = 8000 W = 8 kW.
Všimněme si ale důležitého momentu. Vztah $P = Fs/t$ můžeme přeci zapsat jako
$P = Fs/t = Fv$
Tedy výkon odpovídá součinu síly na těleso a jeho rychlosti. Rychlost je v našem případě 20 m/s a výkon je tedy prostě součin síly 400 N a rychlosti 20 m/s, čili 8000 W.
Výsledek: 8000 W
ID: 231;
Tags: výkon, t-vykon;
Autor: Marek Scholz (admin);
Position: 7/9;
▮
Tažná síla motoru
#232,
Marek Scholz (admin),
pos:7/9,
kat
Stará Škoda Fabia má maximální výkon motoru 54 kW. Šine si to po dálnici nepovolenou rychlostí 144 km/h. Jak velkou silou motor pohání auto?
Řešení: P = 54 kW; v = 144 km/h = 40 m/s; F = ?;
Základní vztah je $P = F \cdot v$. Obě strany vzdělíme rychlostí $v$ a dostaneme
$F = P/v$ = 54000 W / 40 m/s = 1350 N.
To je hodně, to je jako kdyby auto přes kladku vytahovalo závaží hmotnosti 135 kg!
Výsledek: 1350 N
ID: 232;
Tags: výkon, t-vykon;
Autor: Marek Scholz (admin);
Position: 7/9;
▮
Spotřeba lednice
#234,
Marek Scholz (admin),
pos:6/9,
kat
Helmut má velkou lednici s průměrným příkonem 150 W. Kolik zaplatí za její provoz za celý rok, pokud cena elektřiny je 5 kč/kWh?
Řešení: Příkon vyjádříme v kW a rok v hodinách. Pak máme:
E = Pt = 0,15 kW * (365 * 24 h) = 1314 kWh.
Za každý kWh zaplatíme 5 kč, čili náklady jsou 5*1314 kč = 6570 kč.
Výsledek: 6570 kč
Hint: Vyjádřete, kolik hodin má rok.
ID: 234;
Tags: výkon, t-vykon;
Autor: Marek Scholz (admin);
Position: 6/9;
▮
Spotřeba televize
#286,
Marek Scholz (admin),
pos:5/9,
kat
Pan Hňup má velkou televizní obrazovku s příkonem 300 W. Ta běží v průměru 4 hodiny denně. Pana Hňupa by zajímalo, kolik zaplatí za spotřebu elektrické energie za měsíc leden, pokud je cena 5,50 Kč/kWh.
Řešení:
Výsledek: 204,6 Kč
ID: 286;
Tags: ;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
přitahování Země a Měsíce
#254,
Marek Scholz (admin),
pos:1/9,
kat
Země a Měsíc na sebe vzájemně působí gravitační silou. Co je větší, síla kterou Země působí na Měsíc, nebo síla kterou Měsíc působí na Zemi?
Řešení:
Výsledek: stejně velké síly opačného směru
ID: 254;
Tags: t-gravitacni-zakon;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Přeči gravitační zákon
#255,
Marek Scholz (admin),
pos:1/9,
kat
Vyberte správné tvrzení´vyjadřující Newtonův gravitační zákon
ID: 255;
Tags: t-gravitacni-zakon;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Hodnota gravitační konstanty
#256,
Marek Scholz (admin),
pos:1/9,
kat
Hodnota gravitační konstanty G, která vystupuje v Newtonové gravitačním zákoně, je
ID: 256;
Tags: t-gravitacni-zakon;
Autor: Marek Scholz (admin);
Position: 1/9;








