Vítejte! Tato stránka slouží jako databáze řešených fyzikálních úloh pro střední a základní školy.
▮
Práce při zvedání kýble
#147,
Marek Scholz (admin),
pos:1/9,
kat
Jak velkou práci vykonám, když rovnoměrně zvednu kýbl s vodou o hmotnosti 5 kg do výšky 60 cm?
Uvažujte g = 10 m/s2
Řešení: $W = F \cdot s = 50\,\mathrm{N} \cdot 0,6\,\mathrm{m} = 30\,\mathrm{J}$.
Výsledek: 30 J
Hint: Nezapomeňte převést na základní jednotku.
ID: 147;
Tags: práce,t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Práce při tlačení bedny
#148,
Marek Scholz (admin),
pos:1/9,
kat
Pan Šňup obdržel velkou a těžkou krabici s banány, o hmotnosti 20 kg. Potřebuje ji po podlaze přesunout na druhou stranu místonosti do vzdálenosti 8 m. Koeficient tření mezi podlahou a krabicí je roven 0,3. Určete velikost práce, kterou pan Šňup musí vykonat.
Řešení: Síla pana Šňupa musí překonávat třecí sílu, pro rovnoměrné tlačení krabice tak potřebuje vyvinout sílu právě rovnou třecí síle.
Velikost smykové třecí síly je
$F_t = f \cdot F_n = fmg = 0,3 \cdot 200\,\mathrm{N} = 60\,\mathrm{N}$
$W = F \cdot s = F_t \cdot s = 60\,\mathrm{N} \cdot 8\,\mathrm{m} = 480\,\mathrm{J}$
Vykoná práci 480 J.
Výsledek: 480 J
Hint: Pan Šňup musí působit silou stejně velkou, jako je smyková třecí síla.
ID: 148;
Tags: práce, t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Tři síly na vozík
#149,
Marek Scholz (admin),
pos:1/9,
kat
Na kolejích stojí těžký vozík. Ciri, Geralt a Yennefer na vozík působí silami F1, F2 a F3 a tlačí ho po kolejích. Velikosti sil jsou shodné. Kdo z nich koná nulovou užitečnou práci?
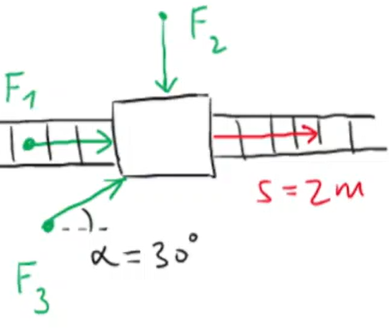
obr.
skrýt |
S |
M |
L
Řešení:
Výsledek: Nulovou práci koná Geralt (F2), působí kolmo na posunutí.
ID: 149;
Tags: práce, rozklad sil, t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Práce s pytlem cementu
#151,
Marek Scholz (admin),
pos:1/9,
kat
Helmut staví dům. Pomocí jednoduché kladky a lana zvedá pytel cementu o hmotnosti 15 kg z původní výšky 3 m do finální výšky 10 metrů. Jak velkou práci při tom vykoná?
Řešení: Stačí si jen uvědomit, že pytel se posune o 7 metrů. Potom
$W = F \cdot s = 150\,\mathrm{N} \cdot 7\,\mathrm{m} = 1050\,\mathrm{J}.
Výsledek: 1050 J
ID: 151;
Tags: práce, t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Hnací síla auta
#26,
Marek Scholz (admin),
pos:1/9,
kat
Auto při jízdě po dálnici spotřebuje asi 8 litrů benzínu na 100 km. Z jednoho litru zužitkuje na pohon energii asi 10 MJ. Jak velká síla pohání auto a překonává odpor vzduchu a valivý odpor?
Řešení: Z osmi litrů může motor vykonat práci o velikosti 80 MJ. Jelikož je W = Fs, tak
$F = W/s = 8\times10^7\,\text{J} / 10^5\,\text{m} = 800\,\text{N}$.
Výsledek: 800 N
Hint: Použijte bezostyšně W = Fs.
ID: 26;
Tags: práce,t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Práce šikmé síly
#150,
Marek Scholz (admin),
pos:1/9,
kat
Na kolejích stojí těžký zarezlý vozík. Ciri, Geralt a Yennefer na vozík působí silami F1, F2 a F3 a tlačí ho po kolejích. Jak velkou práci při tlačení vykoná Yennefer (F3), když působí silou o velikosti 300 N ve vyznačeném směru a dojde k posunu vozíku o dva metry?

obr.
skrýt |
S |
M |
L
Řešení: Velikost složky síly F3, která působí ve směru pohybu, označme $F_p$.
Síla působí pod úhlem 30° oproti směru posunutí a složka síly ve směru posunutí má proto velikost
$F_p = F_3 \cdot \cos30° = 300\,\mathrm{N} \cdot 0,866 = 260\,\mathrm{N}$.
Práce potom je
$W = F_p \cdot s = 260\,\mathrm{N} \cdot 2\,\mathrm{m} = 520\,\mathrm{J}$.
Výsledek: 520 J
Hint: Musíte nejprve určit velikost složky síly F3, která působí ve směru pohybu.
ID: 150;
Tags: práce, rozklad sil, t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Vztah pro práci
#152,
Marek Scholz (admin),
pos:1/9,
kat
Taylor Swift potřebuje zvednout těžký vergl ze země do výšky $h$ a položit ho na stůl. Vergl má hmotnost $m$, koeficient tření mezi podlahou a podrážkami je $f$, šířka desky stolu je $s$. Podle jakého vztahu můžeme určit množství vykonané práce při zvednutí?
Řešení:
Výsledek: W = mgh
ID: 152;
Tags: práce, t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Držení činky
#238,
Marek Scholz (admin),
pos:1/9,
kat
Držím činku o hmotnosti 5 kg ve výšce 1,5 m nad zemí po dobu jedné minuty. Jak velkou práci vykonám? Co kdybych činku nedržel a místo toho ji položil na skříň? Jakou práci vykoná skříň? Liší se v něčem tyto situace? Diskutujte.
Řešení: Aby byla konána fyzikální práce, tak na těleso (zde činku) musí působit síla a musí tam být také nějaké posunutí (ve směru či proti směru síly). Pokud bych činku držel skutečně dokonale na jednom místě, tak by vykonaná práce na čince byla nulová, protože posunutí je nulové. Tak by to jistě bylo, kdybychom postavili činku na stůl. Při držení pomocí svalů se ale činka ve skutečnosti trochu hýbe - svaly a ruce se nám trošičku klepou, takže tam jsou malá posunutí tam a zpět. Když činku o kousíček posuneme nahoru, konáme kladnou práci na čince, když ji brzdíme při pohybu dolů, konáme na čince malou zápronou práci. Svaly ale pak práci konají, spotřebovávají energii a časem se unaví.
Výsledek:
ID: 238;
Tags: práce, t-prace;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Práce s půllitrem
#207,
Marek Scholz (admin),
pos:2/9,
kat
Ze stolu o výšce 70 cm zvedáte půllitr s limonádou o hmotnosti 800 g. Určete, do jaké výšky nad zemí byste museli zvednout půllitr, abyste vykonali práci o velikosti 6 J? Uvažujte g = 10 m/s2.
Uveďte v centimetrech.
Řešení: Práce při zvedání tělesa proti gravitaci se rovná přírůstku potenciální energie:
$W = m g (h - h_0)$
Kde:
- $W = 6\ \text{J}$
- $m = 0{,}8\ \text{kg}$
- $g = 10\ \text{m/s}^2$
- $h_0 = 0{,}70\ \text{m}$ (výška stolu)
- $h$ = hledaná výška nad zemí
Dosadíme:
$6 = 0{,}8 \cdot 10 \cdot (h - 0{,}70)$
$6 = 8(h - 0{,}70)$
$\frac{6}{8} = h - 0{,}70$
$0{,}75 = h - 0{,}70$
$h = 0{,}75 + 0{,}70 = 1{,}45\ \text{m}$
Půllitr musíte zvednout do výšky 1,45 metru nad zemí.
Výsledek: 145 cm
ID: 207;
Tags: potenciální energie, t-potencialni-energie;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Potenciální energie paní Mrtvé
#217,
Marek Scholz (admin),
pos:2/9,
kat
Paní Mrtvá stojí na zemi v pátém patře (páté nadzemní podlaží), ve výšce 13 m nad silnicí. Určete velikost její potenciální energie vůči
a) silnici
b) vůči panu Živnému, který bydlí ve druhém patře.
c) vůči podlaze bytu paní Mrtvé.
d) vůči stropu jejího bytu
e) vůči paní Zkyslé, která bydlí o patro výš.
Všechny potřebné vzdálenosti, výšky a další údaje rozumně odhadněte.
Řešení: Budiž hmotnost paní Mrtvé 60 kg. Potenciální energii vždy určíme ze vztahu $E_p = mgh$.
Vždy ale musíme určit, vůči čemu odměřujeme výšku.
Paní Mrtvá má těžiště zhruba 1 m nad podlahou. Odtud odvodíme, že výška patra jsou zhruba 3 metry.
a) vůči silnici - 60 x 10 x 13 = 7800 J
b) vůči panu Živnému, který bydlí ve druhém patře - dělí je 3 patra, výškový rozdíl je 9 metrů, čili 60 x 10 x 9 = 5400 J.
c) vůči podlaze bytu paní Mrtvé - těžiště jeden metr nad podlahou, čili 600 J.
d) vůči stropu jejího bytu - paní Mrtvá je pod stropem ve výšce asi 2 metry. Světe div se, její potenciální energie vůči stropu bude záporná v hodnotě -1200 J
e) vůči paní Zkyslé, která bydlí o patro výš - výška patra 3 metry, čili potenciální energie paní Mrtvé je -1800 J.
Výsledek:
ID: 217;
Tags: potenciální energie, t-potencialni-energie;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Stoupání na tatranku
#183,
Marek Scholz (admin),
pos:2/9,
kat
Princezna Fakana se chystá vystoupat na nejvyšší horu království a pozdravit tam obra Mamlmuta. Princezna začíná strmý výšlap v nadmořské výšce 500 m.n.m., kde snědla tatranku s energetickým obsahem 1100 kJ. Do jaké nadmořské výšky vystoupá na energii této tatranky, pokud bychom předpokládali, že 20% z energetického obsahu tatranky přemění na svoje stoupání? Princezna má hmotnost 60 kg.

obr.
skrýt |
S |
M |
L
Uvažujte g=10 m/s2.
Řešení:
Výsledek: 867 m.n.m.
ID: 183;
Tags: potenciální energie, t-potencialni-energie;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Potenciální energie ve velké výšce
#235,
Marek Scholz (admin),
pos:2/9,
kat
Kolikrát větší je potenciální energie družice ve výšce 1000 km nad povrchem Země než potenciální energie stejné družice ve výšce 500 km nad povrchem?
ID: 235;
Tags: potenciální energie, t-potencialni-energie;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Kinetická energie při pádu
#181,
Marek Scholz (admin),
pos:3/9,
kat
Zkušený skokan Helmut skáče do vody z výšky 40 m. Jakou velikost bude mít jeho kinetická energie dvě sekundy po seskoku? Helmut nechť má hmotnost 70 kg. Odpor vzduchu zanedbejte a pokud použijete nějaký fyzikální parametr, užijte co nejpřesnější hodnotu.
Řešení: Dvě sekundy po seskoku bude mít rychlost $v = 2g$ = 19,62 m/s.
Z toho plyne kinetická energie
$E_k = \frac{1}{2}mv^2$ = $\frac{1}{2} \cdot 70\,\mathrm{kg} \cdot (30\,\mathrm{m/s})^2$ = 13473 J.
Výsledek: 13473 J
ID: 181;
Tags: kinetická energie, t-kineticka-energie;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Kinetická energie míče
#185,
Marek Scholz (admin),
pos:3/9,
kat
Jakou rychlostí byste museli vykopnout fotbalový míč, aby jeho kinetická energie byla 1 kJ? Je to realistické?
Pro číselný výpočet uvažujte hmotnost fotbalového míče 420 g.
Řešení: $E_k = \frac{1}{2}mv^2$
Vyjádříme $v$:
$v = \sqrt{2E_k/m}$ $= \sqrt{2000\,\mathrm{J} / 0.42\,\mathrm{kg}} = 69\,\mathrm{m/s}$.
To je 248 km/h a je to již pravděpodobně nad běžné lidské možnosti.
Výsledek: 69 m/s
ID: 185;
Tags: kinetická energie, pohybová energie, t-kineticka-energie;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Benzin na předjíždění
#182,
Marek Scholz (admin),
pos:3/9,
kat
Osobní auto při předjíždění zrychlilo ze 72 km/h na 108 km/h. Víme, že ze spálení jednoho litru benzínu se na pohyb auta využije energie o velikosti asi 10 MJ. Vypočítejte, kolik nás bude stát benzín spotřebovaný na toto předjíždění.
Pro číselný výpočet uvažujte hmotnost auta 1,5 tuny a cenu benzínu 35 kč/litr. Uveďte s přesností na desetiny koruny.
Hint: Převeďte na m/s. Určete koncovou a počáteční kinetickou energii a následně spočtěte rozdíl.
ID: 182;
Tags: kinetická energie, t-kineticka-energie;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Kolik atomovek na asteroid
#211,
Marek Scholz (admin),
pos:3/9,
kat
Před 66 miliony let na Zemi dopadl asteroid o průměru asi 10 km, což způsobilo vyhynutí mnoha druhů. Kolika bombám z Hirošimy to odpovídá? Při výbuchu atomové bomby v Hirošimě se uvolnilo 63 TJ energie. Hustotu asteroidu uvažujte 3500 kg/m3. (Předpokládá se, že k úplnému zániku veškerého života by došlo při impaktu asteroidu o průměru asi 90 km. Pokud je asteroid menší než 25 m, tak pravděpodobně zanikne již v atmosféře a způsobí jen relativně malé škody).
Řešení: **Zadání:**
- Průměr asteroidu: $d = 10\ \text{km} = 10\,000\ \text{m}$
- Hustota asteroidu: $\rho \approx 3500\ \text{kg/m}^3$
- Rychlost dopadu: $v = 18\,000\ \text{m/s}$
- Energie jedné bomby z Hirošimy: $E_{\text{Hirošima}} = 63 \cdot 10^{12}\ \text{J}$
** 1. Výpočet kinetické energie asteroidu **
Objem koule:
$V = \frac{4}{3} \pi r^3 = \frac{4}{3} \pi \left( \frac{d}{2} \right)^3 = \frac{4}{3} \pi \left(5000\right)^3$
$V \approx \frac{4}{3} \pi \cdot 1{,}25 \cdot 10^{11} \approx 5{,}24 \cdot 10^{11}\ \text{m}^3$
Hmotnost asteroidu:
$m = \rho V = 3500 \cdot 5{,}24 \cdot 10^{11} \approx 1{,}83 \cdot 10^{15}\ \text{kg}$
Kinetická energie (dosazení v základních jednotkách):
$E = \frac{1}{2} m v^2 = \frac{1}{2} \cdot 1{,}83 \cdot 10^{15} \cdot (1{,}8 \cdot 10^4)^2$
$E \approx 0{,}5 \cdot 1{,}83 \cdot 10^{15} \cdot 3{,}24 \cdot 10^8 \approx 2{,}96 \cdot 10^{23}\ \text{J}$
** 2. Kolika bombám z Hirošimy to odpovídá? **
Počet bomb:
$\frac{2{,}96 \cdot 10^{23}}{63 \cdot 10^{12}} \approx 4{,}7 \cdot 10^{9}$
**Odpověď:**
Dopad asteroidu o průměru 10 km uvolnil energii přibližně **4,7 miliardy krát větší**, než výbuch atomové bomby v Hirošimě.
Výsledek: 4700000000 -krát
ID: 211;
Tags: kinetická energie, t-kineticka-energie;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Nepovolená rychlost
#236,
Marek Scholz (admin),
pos:3/9,
kat
Pan Šmejd jel v obci nepovolenou rychlostí 70 km/h, namísto aby jel 50 km/h. O kolik procent byla jeho kinetická energie větší, než kdyby jel podle předpisů?
Řešení: Ve vztahu pro kinetickou energii je rychlost ve druhé mocnině. Poměr skutečné a povolené rychlosti je 7/5. Kinetická energie bude větší faktorem $(7/5)^2 = 1,96$.
Kinetická energi vzroste o 96 %.
Výsledek: 96 %
ID: 236;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Snížení kinetické energie
#237,
Marek Scholz (admin),
pos:3/9,
kat
Paní Kerblíková jede na kole. O kolik procent by musela snížit svoji rychlost, aby její kinetická energie klesla o 50%?
Řešení: Kinetická energie je úměrná druhé mocnině rychlosti a tedy rychlost je úměrná odmocnině z kinetické energie. Pokud je původní kinetická energie rovna 1, tak nová je 1/2, a pokud je původní rychlost 1, tak nová rychlost bude $\sqrt{1/2} = 0,707$.
Změna rychlosti pak je 1-0,707 = 0,293.
Čili musí snížit rychlost of 29,3%.
Výsledek: 29,2 %
ID: 237;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Dopad asteroidu
#209,
Marek Scholz (admin),
pos:3/9,
kat
Při výbuchu atomové bomby v Hirošimě se uvolnilo 63 TJ energie. Typická rychlost dopadu asteroidů do atmosféry je 18 km/s a asteroidy bývají ze směsice kamene a železa. Odhadněte výpočtem, jaký průměr by musel být asteroid, aby při jeho dopadu byla uvolněna energie jako v Hirošimě.
Řešení: ### Odhad velikosti asteroidu s energií výbuchu atomové bomby v Hirošimě
**Zadání:**
- Uvolněná energie: $E = 63\ \text{TJ} = 6{,}3 \cdot 10^{13}\ \text{J}$
- Rychlost dopadu: $v = 18\ \text{km/s} = 18{,}000\ \text{m/s}$
- Hustota asteroidu (kámen + železo): $\rho \approx 3500\ \text{kg/m}^3$
- Hledáme průměr $d$ asteroidu (předpokládáme kulový tvar)
**1. Kinetická energie asteroidu při dopadu:**
$E = \frac{1}{2}mv^2$
Dosadíme za hmotnost tělesa hmotnost koule:
$m = \rho V = \rho \cdot \frac{4}{3}\pi r^3 = \rho \cdot \frac{4}{3}\pi \left( \frac{d}{2} \right)^3$
$\Rightarrow E = \frac{1}{2} \cdot \rho \cdot \frac{4}{3}\pi \left( \frac{d}{2} \right)^3 \cdot v^2$
$\Rightarrow E = \frac{\pi}{6} \cdot \rho \cdot d^3 \cdot v^2$
**2. Vyjádříme průměr $d$ z rovnice:**
$d^3 = \frac{6E}{\pi \rho v^2}$
Dosadíme hodnoty:
$d^3 = \frac{6 \cdot 6{,}3 \cdot 10^{13}}{\pi \cdot 3500 \cdot (1{,}8 \cdot 10^4)^2}$
Spočítáme:
$(1{,}8 \cdot 10^4)^2 = 3{,}24 \cdot 10^8$
$\pi \cdot 3500 \cdot 3{,}24 \cdot 10^8 \approx 3{,}57 \cdot 10^{12}$
Čitatel: $6 \cdot 6{,}3 \cdot 10^{13} = 3{,}78 \cdot 10^{14}$
$\Rightarrow d^3 = \frac{3{,}78 \cdot 10^{14}}{3{,}57 \cdot 10^{12}} \approx 106$
$\Rightarrow d \approx \sqrt[3]{106} \approx 4{,}75\ \text{m}$
Odpověď:
Aby měl dopad asteroidu stejnou energii jako výbuch atomové bomby v Hirošimě, musel by mít asteroid průměr přibližně 4,75 metru.
Výsledek: Aby měl dopad asteroidu stejnou energii jako výbuch atomové bomby v Hirošimě, musel by mít asteroid
Hint: Odhadněte hustotu asteroidu na základě jeho materiálového složení. Napište si vztah pro kinetickou energii a za hmotnost dosaďte hustotu a poloměr. Vyjádřete poloměr.
ID: 209;
Tags: kinetická energie, t-kineticka-energie;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Elektrárna na potenciální energii
#208,
Marek Scholz (admin),
pos:4/9,
kat
Víte, ve kterém typy elektráren se využívá přeměny tíhové potenciální energie na kinetickou energii a nakonec na elektrickou energii. Popište, jak se v elektrárně tyto energie v sebe proměňují.
Řešení: Vodní elektrárna či přečerpávací elektrárna. Voda klesá a ztrácí potenciální energii, přitom roztáčí turbínu (kinetická energie). Turbína roztáčí generátor střídavého proudu. To už je ale jiný příběh.
Výsledek:
ID: 208;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Odrazy tenisového míčku
#230,
Marek Scholz (admin),
pos:4/9,
kat
Imhotep zvedl tenisový míček a pustil ho na podlahu. Míček na podlaze skákal, ale po každém odrazu vyskočil trochu méně. Popište podrobně všechny přeměny energie, ke kterým docházelo od okamžiku vypuštění míčku až do okamžiku kdy míček po odrazu zase vystoupal do nejvyššího bodu.
ID: 230;
Tags: t-ZZME, zákon zachování mechanické energie;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Skokan o tyči
#210,
Marek Scholz (admin),
pos:4/9,
kat
Popište podrobně všechny přeměny energie, ke kterým dochází během skoku o tyči. Od okamžiku, kdy skokan stojí na startu až do okamžiku, kdy stojí na dopadové matraci a zdraví publikum.
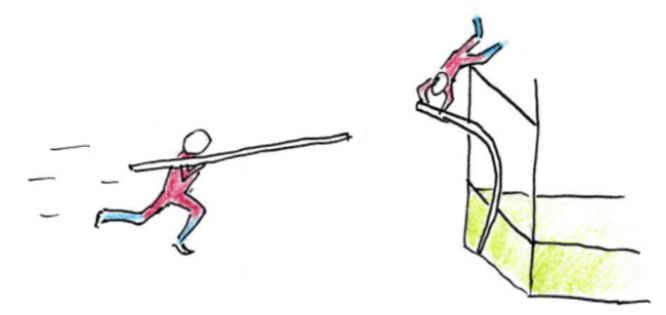
obr.
skrýt |
S |
M |
L
Řešení: Stojí na startu - chemická energie molekul ve svalech. Svaly pak konají práci - roste kinetická energie běžce. Když zapíchne tyčku, tak se tyčka začne ohýbat a kinetická energie běžce se přeměňuje na deformační energii uloženou v tyčce. Poté když skokan stoupá nahoru se deformační energie tyčky přeměňuje na tíhovou potenciální energii skokana. Když překonává nahoře laťku, tak dosáhl maxima potenciální tíhové energie a ta se pak postupně přeměňuje na kinetickou energii, jak se zrychluje jeho pád. Nakonec při dopadu na žíněnku se kinetická přemění na teplo a částečně i na zvukovou energii. Při dopadu se totiž žíněnka i skokan trošku zahřejí.
Výsledek:
ID: 210;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Pád ze třetího patra
#194,
Marek Scholz (admin),
pos:5/9,
kat
Ve filmu Copak je to za vojáka skáče vojín Kouba ze třetího patra, aby se včas dostal na nástup jednotky. Pokud by tak učinil, jaká bude jeho rychlost při dopadu na zem? Řešte na základě zákona zachování mechanické energie.
Pro výpočet uvažujte, že skáče z výšky 7 metrů. $g = 9,81\,\mathrm{m/s^2}$.
Řešení: Při skoku ze třetího patra máme dvě patra pod sebou. Výška patra bývá okolo 3 m a při skoku z okna tak lze odhadnout, že výška nad zemí je třeba 7 metrů.
Zákon zachování energie říká, že součet potenciální a kinetické na začátku i na konci bude stejný:
$E_{p1} + E_{k1} = E_{p2} + E_{k2}$
Počáteční kinetická energie je nulová, stejně tak jako koncová potenciální energie. Tedy:
$E_{p1} + 0 = 0 + E_{k2}$
Čili vztah se redukuje na
$mgh = \frac{1}{2}mv^2$,
což odpovídá tomu, že se Veškerá potenciální energie přemění na kinetickou energii. Neznámá je rychlost $v$, kterou chceme ze vztahu osamostatnit.
V první řadě si všimneme, že na obou stranách můžeme vykrátit hmotnost a dostaneme
$gh = \frac{1}{2}v^2$
Obě strany násobíme dvěma a máme
$2gh = v^2$
čili
$v = \sqrt{2gh}$ $= \sqrt{2 \cdot 9,8\,\mathrm{m/s^2} \cdot 7\,\mathrm{m}}$ = 11,7 m/s = 42,2 km/h.
Je to hodně nebo málo? Zkuste někdy jít pomalou chůzí rychlostí 2 km/h a jen tak narazit do stěny. Uvidíte, jak se potlučete...
Výsledek: 11,7 m/s
ID: 194;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Helmut kope na Marsu
#213,
Marek Scholz (admin),
pos:5/9,
kat
Helmut byl na dovolené na Měsící. Vystřelil vzhůru tenisový míček rychlostí 40 m/s. Určete, do jaké výšky vystoupá, použijte zákon zachování energie.
Řešení: Zákon zachování energie:
$\frac{1}{2} m v_1^2 + m g' h_1 = \frac{1}{2} m v_2^2 + m g' h_2$
se zjednoduší, protože je počáteční výška nulová a koncová rychlost je nulová, čili
$\frac{1}{2} m v_1^2 = m g h_2$
Buď rovnou dosadíme a potom vyjádříme $h_2$, nebo vyjádříme ještě "s písmenky".
Samozřejmě po cestě krátíme $m$:
$h_2 = v_1^2/2g$
Dosadíme v základních jednotkách, přičemž gravitační zrychlení na Měsící je $g = 1,62\,\mathrm{m/s^2}$:
$h_2 = 40^2/3,24 = 494\,\mathrm{m}$.
Vystoupá do výšky 494 metrů! To je překvapivě hodně vysoko.
Výsledek: 494 m
ID: 213;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Propad kamene
#27,
Marek Scholz (admin),
pos:5/9,
kat
Ve výšce 10 m nad zemí kámen o hmotnosti 200 g padá rychlostí 5 m/s. Jakou rychlostí bude padat ve výšce 8 m nad zemí? Odpor vzduchu zanedbejte, uvažujte g=10 m/s2.
Řešení: Protože odpor vzduchu zanedbáváme, platí zákon zachování mechanické energie $E_1 = E_2$. Rovnice je tedy:
$\frac{1}{2} m v_1^2 + m g h_1 = \frac{1}{2} m v_2^2 + m g h_2$
V tuto chvíli bychom do vztahu mohli dosadit všechny známé hodnoty a vyjádřit finální rychlost. Zde si však ještě ponecháme písmenka a vyjádříme rychlost $v_2^2$ obecně:
$\frac{1}{2} m v_2^2 = \frac{1}{2} m v_1^2 + m g h_1 - m g h_2$
$m$ se pokrátí a dostaneme:
$v_2^2 = v_1^2 + 2 g (h_1 - h_2)$
Dosadíme známé hodnoty:
$v_2^2 = 5^2 + 2 \cdot 10 \cdot (10 - 8) = 65$
$v_2 = \sqrt{65} \approx 8{,}06 \, \text{m/s}$
Výsledek: 8,06 m/s
Hint: Součet kinetické a potenciálná tíhové energie na začátku a na konci musí být stejný. Z toho vyplyne rovnice, kde hledaná rychlost bude jediná neznámá.
ID: 27;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Vozík na hrb
#214,
Marek Scholz (admin),
pos:5/9,
kat
Vozík horské dráhy je ve výšce 20 metrů nad zemí a jede rychlostí 15 m/s. Shakiru by zajímalo, jestli takto rozjetý vozík bude schopen překonat hrb ve výšce 35 m nad zemí. Rozhodněte na základě výpočtu. Nakreslete situaci. Uvažujte g = 10 m/s2.
Řešení: Počáteční mechanická energie vozíku je
$E = \frac{1}{2}mv_1^2 + mgh_1$
Výsledek nebude záviset na hmotnosti vozíku a můžu si klidně říci, že má hmotnost 1 kg, i když to zní divně. Pak mi vyjde počáteční mechanická energie 312,5 J.
Ve výšce 35 metrů by ale vozík musel mít energii o velikosti 350 J, kterou nemá. Hrb tedy nepřejede.
Výsledek:
ID: 214;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Shakira na horské dráze
#215,
Marek Scholz (admin),
pos:5/9,
kat
Shakira je na horské dráze jako na obrázku. Zajímá ji, jakou rychlostí bude projíždět nejnižším bodem, pokud její momentální rychlost je 8 m/s. Rozestup mezi výškovými čarami je 5 metrů.
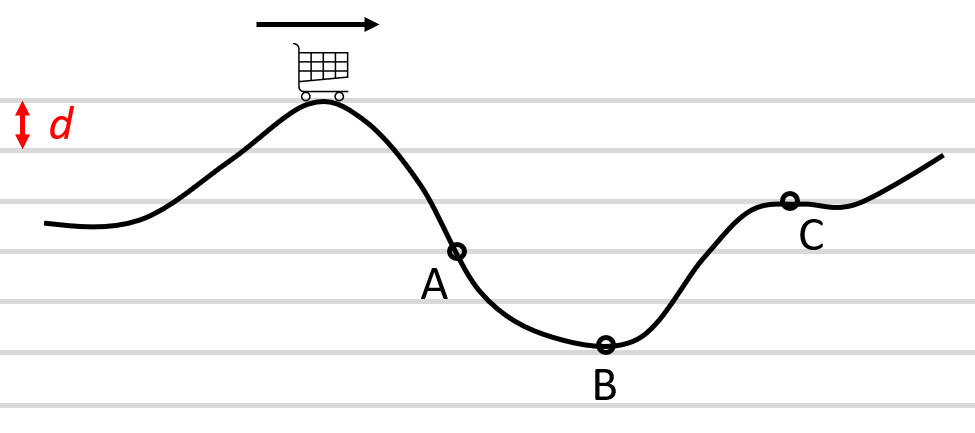
obr.
skrýt |
S |
M |
L
Uvažujte g = 10 m/s2.
Řešení: Protože odpor vzduchu zanedbáváme, platí zákon zachování mechanické energie $E_1 = E_2$. Rovnice je tedy:
$\frac{1}{2} m v_1^2 + m g h_1 = \frac{1}{2} m v_2^2 + m g h_2$
V tuto chvíli bychom do vztahu mohli dosadit všechny známé hodnoty a vyjádřit finální rychlost. Zde si však ještě ponecháme písmenka a vyjádříme rychlost $v_2^2$ obecně:
$\frac{1}{2} m v_2^2 = \frac{1}{2} m v_1^2 + m g h_1 - m g h_2$
$m$ se pokrátí a dostaneme:
$v_2^2 = v_1^2 + 2 g (h_1 - h_2) = v_1^2 + 2 g \Delta h $
Vidíme, že zde vystupuje rozdíl počáteční a koncové výšky. Ten je v našem případě 25 m. Dosadíme
$v_2^2 = 8^2 + 2 \cdot 10 \cdot 25
$v_2 = \sqrt{564} \approx 23{,}7 \, \text{m/s}$.
To už je slušná rychlost (85 km/h).
Výsledek: 23,7 m/s
ID: 215;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Grafy energií při pádu
#233,
Marek Scholz (admin),
pos:5/9,
kat
Z mrakodrapu upustíme peněženku (odpor vzduchu zanedbáme). Jaký přibližný tvar budou mít následující grafy?
a) graf $E_p$ v závislosti na výšce nad zemí?
b) graf $E_k$ v závislosti na výšce nad zemí?
c) graf $E_p$ v závislosti na čase?
d) graf $E_k$ v závislosti na čase?
e) graf rychlosti v závislosti na výšce nad zemí?
f) graf rychlosti v závislosti na čase?
Přiřaďte

obr.
skrýt |
S |
M |
L
ID: 233;
Tags: t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Výstřel na Měsíci
#212,
Marek Scholz (admin),
pos:5/9,
kat
Helmut byl na dovolené na Měsíci. Kolmo vzhůru vykopl míč počáteční rychlostí $v_0$. Ve výšce $h_1$ = 100 m nad povrchem byla rychlost míče $v_1$ = 15 m/s. V jaké výšce nad povrchem byla rychlost míče poloviční oproti počáteční rychlosti?
Řešení: **Zadání:**
- Ve výšce $h_1 = 100\ \text{m}$ je rychlost $v_1 = 240\ \text{m/s}$
- Hledáme výšku $h$, kde $v = \frac{1}{2}v_0$
- Gravitační zrychlení na Měsíci: $g_M \approx 1{,}62\ \text{m/s}^2$
Musíme nejdříve určit počáteční rychlost $v_0$. Ze zákona zachování energie platí
Pro tu platí:
$\frac{1}{2}v_0^2 = \frac{1}{2}v_1^2 + g_M h_1$.
čili
$v_0 = \sqrt{v_1^2 + 2 g_M h_1}$
Dosadíme a máme $v_0$ = 23,43 m/s.
Chceme vědět, v jaké výšce $h$ bude rychlost poloviční. Ze zákona zachování energie mezi počátečním stavem a koncovým stavem plyne:
$ \frac{1}{2}v_0^2 = \frac{1}{2}(v_0/2)^2 + g_M h$.
Výjádříme $h$:
$h = \frac{3}{8} \cdot \frac{v_0^2}{g_M}$
Dosazením za $v_0$ máme $h$ = 127,1 m.
Také můžeme dosadit za $v_0$ z předchozího vztahu a dostaneme
$h = \frac{3}{8} \cdot \frac{v_1^2 + 2 g_M h_1}{g_M}$ = $\frac{3}{8} \cdot (\frac{v_1^2}{g_M} + 2 h_1)$
což po dosazení dá stejný výsledek.
Ve výšce 127 m bude rychlost míče poloviční oproti počáteční.
Výsledek: 127,1 m
ID: 212;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Habakukovo kyvadlo
#216,
Marek Scholz (admin),
pos:5/9,
kat
Habakuk zavěsil kovovou kuličku na 1 metr dlouhý provázek, čímž dostal kyvadlo. Kyvadlo pak vychýlil o úhel 20°z rovnovážné polohy a pustil. Zajímá ho, jaké největší rychlosti kulička během kývání dosáhne. Odpor vzduchu zanedbáme a budeme uvažovat g = 10 m/s2.

obr.
skrýt |
S |
M |
L
Řešení: V nejvyšším bodě má kulička pouze potenciální energii (vzhledem k nejnižší poloze), v dolní části se tato energie přemění na kinetickou. Pomocí zákona zachování mechanické energie tedy platí:
$$
mgh = \frac{1}{2}mv^2
$$
Zkrátíme hmotnost:
$$
gh = \frac{1}{2}v^2 \Rightarrow v = \sqrt{2gh}
$$
Musíme ale nejprve určit výšku $h$, o kterou se kulička zvedla při výchylce.
Když si dobře nakreslíte obrázek, tak zjistíte, že počáteční výška nad rovnovážnou polohou musí být
$h = L(1 - \cos\alpha)$,
kde $L$ je délka závěsu a $\alpha$ úhel náklonu.
Pro naše zadané hodnoty vyjde $h$ = 0,060 m = 6 cm.
Dosazením máme
$v = \sqrt{2gh} = \sqrt{2 \cdot 10 \cdot 0,06}$ = 1,1 m/s.
Rychlost průchodu nejnižším bodem bude zhruba 1,1 m/s.
Výsledek: 1,1 m/s
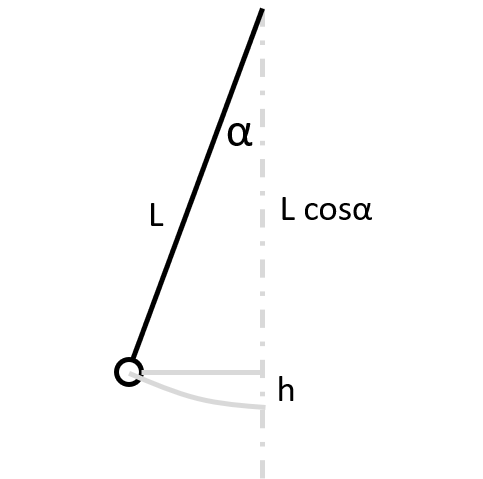
obr.
skrýt |
S |
M |
L
Hint: Potřebujete určit, v jaké výšce nad rovnovážnou polohou kulička na začátku je. K tomu bude potřeba vědět, jaká je svislá vzdálenost kuličky od místa závěsu. K tomu si nakreslete trojúhelník a využijte goniometrickou funkci.
ID: 216;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Hatšepsutino kyvadlo
#218,
Marek Scholz (admin),
pos:5/9,
kat
Hatšepsut zavěsila kovovou kuličku na 2 metry dlouhý provázek, který zavěsila ke stropu, čímž dostala kyvadlo. Kyvadlo pak vychýlila a kuličce udělila počáteční rychlost 0,5 m/s a nechala ji kývat. Počáteční úhel vychýlení byl 30° z rovnovážné polohy. Hatšepsut by zajímalo, do jakého maximálního úhlu se kyvadlo vychýlí po průchodu rovnovážnou polohou.
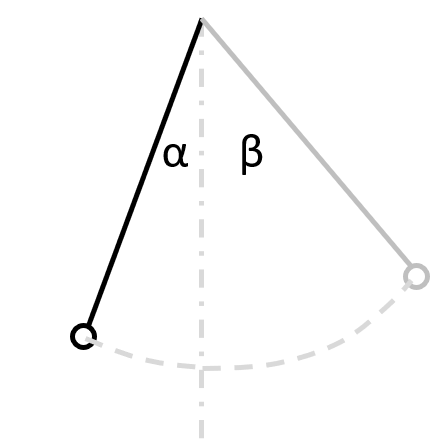
obr.
skrýt |
S |
M |
L
Řešení:
Výsledek:

obr.
skrýt |
S |
M |
L
ID: 218;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Grafy energií
#219,
Marek Scholz (admin),
pos:5/9,
kat
Z okna mrakodrapu ve výšce 80 metrů nad zemí spadnul květináč o hmotnosti 2 kg. Zakreslete co nejpřesněji:
a) Graf, kde znázorníte, jak se mění $E_p$ a $E_k$ v závislosti na výšce kamene nad zemí.
b) Graf, kde znázorníte, jak se mění $E_p$ a $E_k$ v závislosti na čase od vypuštění.
c) Graf, kde znázorníte, jak se mění rychlost květináče v závislosti na čase od vypuštění.
ID: 219;
Tags: zákon zachování mechanické energie, t-ZZME;
Autor: Marek Scholz (admin);
Position: 5/9;
▮
Účinnost rychlovarné konvice
#221,
Marek Scholz (admin),
pos:6/9,
kat
Rychlovarná konvice má příkon 1600 W. Ohřívání vody na čaj trvalo 4 minuty a konvice vodě dodala teplo o velikosti 300 kJ. Určete účinnost ohřevu vody v konvici.
Řešení: $P_0 = 1600\,\mathrm{W}$; $t = 4\,\mathrm{min} = 240\,\mathrm{s}$; $W = 300\,\mathrm{kJ}$.
$\eta = W/E = W/(P_0 t)$ = 300000 J / (1600 W * 240 s) = 0,78 = 78%.
Výsledek: 78 %
ID: 221;
Tags: výkon, účinnost, t-vykon;
Autor: Marek Scholz (admin);
Position: 6/9;
▮
Výkon elektromotoru
#222,
Marek Scholz (admin),
pos:6/9,
kat
Výkon elektrického motoru je 2,4 kW a jeho účinnost je 75%. Určete příkon motoru.
Řešení: $\eta = P/P_0$, čili $P_0 = P/\eta$ = 2,4 kW / 0,75 = 3,2 kW.
Výsledek: 3,2 kW
ID: 222;
Tags: výkon, účinnost, t-vykon;
Autor: Marek Scholz (admin);
Position: 6/9;
▮
Kilowatt po celou hodinu
#224,
Marek Scholz (admin),
pos:6/9,
kat
Elektrické topení má příkon 1 kW a běží po dobu jedné hodiny. Jaké množství elektrické energie spotřebuje? Určete v megajoulech.
Řešení: $E = P_0 t$ = 1000 W * 3600 s = 3 600 000 J = 3,6 MJ.
Zároveň ale spotřebovanou energii mohu vyjádřit jako 1 kW * 1 h = 1 kWh.
Tedy topení spotřebuje energii o velikosti 1 kilowatthodina = 3,6 MJ.
Výsledek: 3,6 MJ
ID: 224;
Tags: výkon, t-vykon;
Autor: Marek Scholz (admin);
Position: 6/9;
▮
Spotřeba lednice
#234,
Marek Scholz (admin),
pos:6/9,
kat
Helmut má velkou lednici s průměrným příkonem 150 W. Kolik zaplatí za její provoz za celý rok, pokud cena elektřiny je 5 kč/kWh?
Řešení: Příkon vyjádříme v kW a rok v hodinách. Pak máme:
E = Pt = 0,15 kW * (365 * 24 h) = 1314 kWh.
Za každý kWh zaplatíme 5 kč, čili náklady jsou 5*1314 kč = 6570 kč.
Výsledek: 6570 kč
Hint: Vyjádřete, kolik hodin má rok.
ID: 234;
Tags: výkon, t-vykon;
Autor: Marek Scholz (admin);
Position: 6/9;
▮
Účinnost spalovacího motoru
#220,
Marek Scholz (admin),
pos:6/9,
kat
Auto jelo 1 kilometr do kopce, přičemž tažná síla motoru byla 500 N a spotřeba činila 80 ml benzínu. Spalná energie 1 litru benzínu je asi 35 MJ na litr. Určete účinnost spalovacího motoru (v procentech).
Řešení: Účinnost $\eta = W/E$.
Vykonaná práce $W = Fs$ = 500 kJ = 0,5 MJ.
Spotřebovaná energie $E = 35\,\mathrm{MJ/l}\cdot 0,08\,\mathrm{l} = 2,8\,\mathrm{MJ}.
Potom $\eta = W/E$ = 0,5 MJ / 2,8 MJ = 0,179 = 17,9 %.
Běžné spalovací motory mívají účinnost v rozmezí 20-35 %.
Výsledek: 17,9 %
ID: 220;
Tags: výkon, účinnost, t-vykon;
Autor: Marek Scholz (admin);
Position: 6/9;
▮
Výkonné ponorné čerpadlo
#223,
Marek Scholz (admin),
pos:6/9,
kat
Ponorné čerpadlo ve studni má příkon 4,2 kW a účinnost 60 %. Za jak dlouho vyčerpá 200 litrů vody do výšky 4,5 metru? Uvažujte g = 10 m/s2.
Řešení: $P_0 = 2000\,\mathrm{W}$; $eta = 0,6$; $m = 200\,\mathrm{kg}$; $h = 4,5\,\mathrm{m}$; $t = ?;
Určíme výkon: $P = \eta P_0$ = 1200 W.
Čerpadlo má vykonat práci $W = \Delta E_p = mgh$ = 9000 J.
Jelikož $P = W/t$, tak je
$t = W/P$ = 9000 J / 1200 W = 7,5 s.
Dvěstě litrů vody vyčerpá za 7,5 s. To je slušně výkonné čerpadlo!
Výsledek: 7,5 s
ID: 223;
Tags: výkon, účinnost, t-vykon;
Autor: Marek Scholz (admin);
Position: 6/9;
▮
Výkon motoru
#225,
Marek Scholz (admin),
pos:6/9,
kat
Maximální výkon motoru Markétina Audi je 120 kW a účinnost spalovacího motoru je asi 30%. Kolik benzínu motor spotřebuje za jednu minutu jízdy na plný výkon? Spalné teplo jednoho litru benzínu je asi 30 MJ.
Řešení: Určíme vykonanou práci:
$W = P t = 1,2\times10^5\,\mathrm{W} \cdot 60\,\mathrm{s} = 7,2\times10^6\,\mathrm{J}$ = 7,2 MJ.
Platí $\eta = W/E$. Z toho vyjádříme spotřebovanou energii:
$E = W/\eta$ = 7,2 MJ / 0,3 = 24 MJ.
Spotřeba benzínu v litrech je pak 24 / 30 = 0,8 litru
Výsledek: 0,8 litr
ID: 225;
Tags: výkon, účinnost, t-vykon;
Autor: Marek Scholz (admin);
Position: 6/9;
▮
Výkon motoru
#231,
Marek Scholz (admin),
pos:7/9,
kat
Motor auto pohání silou 400 N, přičemž auto ujede během pěti minut 6 kilometrů. Určete výkon motoru.
Řešení: Zápis: F = 400 N; t = 5 min = 300 s; s = 6 km = 6000 m.
Pro výkon platí:
$P = W/t = Fs/t$ = (400 N * 6000 m) / 300 s = 8000 W = 8 kW.
Všimněme si ale důležitého momentu. Vztah $P = Fs/t$ můžeme přeci zapsat jako
$P = Fs/t = Fv$
Tedy výkon odpovídá součinu síly na těleso a jeho rychlosti. Rychlost je v našem případě 20 m/s a výkon je tedy prostě součin síly 400 N a rychlosti 20 m/s, čili 8000 W.
Výsledek: 8000 W
ID: 231;
Tags: výkon, t-vykon;
Autor: Marek Scholz (admin);
Position: 7/9;
▮
Tažná síla motoru
#232,
Marek Scholz (admin),
pos:7/9,
kat
Stará Škoda Fabia má maximální výkon motoru 54 kW. Šine si to po dálnici nepovolenou rychlostí 144 km/h. Jak velkou silou motor pohání auto?
Řešení: P = 54 kW; v = 144 km/h = 40 m/s; F = ?;
Základní vztah je $P = F \cdot v$. Obě strany vzdělíme rychlostí $v$ a dostaneme
$F = P/v$ = 54000 W / 40 m/s = 1350 N.
To je hodně, to je jako kdyby auto přes kladku vytahovalo závaží hmotnosti 135 kg!
Výsledek: 1350 N
ID: 232;
Tags: výkon, t-vykon;
Autor: Marek Scholz (admin);
Position: 7/9;
▮
Přečerpávací elektrárna
#226,
Marek Scholz (admin),
pos:7/9,
kat
Přečerpávací elektrárna Dlouhé stráně má maximální instalovaný výkon 650 MW, přičemž má spád 510 m. Jaký je objemový průtok vody potrubím (m3/s), pokud je účinnost procesu 70%?
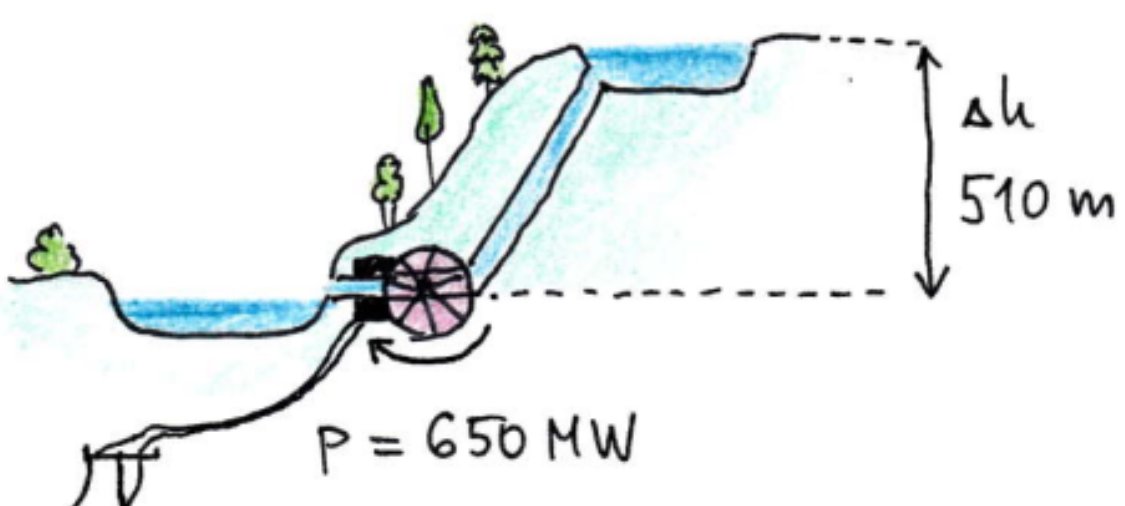
obr.
skrýt |
S |
M |
L
Řešení: P = 650 MW; h = 510 m; $\eta$ = 0,7; $\rho$ = 1000 kg/m3.
Hledáme objemový průtok, který označíme třeba $Q$.
Hmotnost vody, která se v elektrárně přenese za dobu $t$:
$m = \rho V = \rho Q t$
Změna potenciální energie vody za tento čas je
$\Delta E_p = mgh = \rho Q t g h$.
Z toho plyne příkon elektrárny (spotřebovává potenciální energii vody):
$P_0 = \Delta E_p / t = \rho Q g h$.
Známe výkon $P$, čili
$P/\eta = \rho Q g h$.
Vyjádříme neznámý objemový průtok $Q$:
$Q = P / (\eta \rho g h)$ = 185,6 m3/s.
Za sekundu by při maximálním výkonu proteklo 185,6 m3 vody! To je obrovské číslo.
Výsledek: 185,6
ID: 226;
Tags: výkon, účinnost, t-vykon;
Autor: Marek Scholz (admin);
Position: 7/9;
▮
Síla na auto
#229,
Marek Scholz (admin),
pos:7/9,
kat
Spotřeba auta při jízdě na dálnici je asi 8 litrů na 100 km. Jeden litr benzínu obsahuje spalnou energii 30 MJ a účinnost motoru je 25 %. Auto jede rychlostí 124 km/h. Jakou průměrnou velikost má síla, která pohání auto?
ID: 229;
Tags: výkon, t-vykon;
Autor: Marek Scholz (admin);
Position: 7/9;
▮
Výkon při stoupání dodávky
#227,
Marek Scholz (admin),
pos:7/9,
kat
Dodávka o hmotnosti 3 tuny jela po vodorovné silnici stálou rychlostí 54 km/h při výkonu motoru 20 kW. Jaký musí být výkon motoru, pokud pojede stejnou rychlostí do kopce se stoupáním 40 m na kilometr dráhy?
ID: 227;
Tags: výkon, t-vykon;
Autor: Marek Scholz (admin);
Position: 7/9;
▮
Maximální sklon svahu
#228,
Marek Scholz (admin),
pos:7/9,
kat
a) Jaký je maximální sklon dlouhého svahu, aby do něj Škoda Fabia o hmotnosti 1500 kg a výkonu 54 kW mohla jet konstantní rychlostí 30 km/h?
b) Jakou spotřebu benzínu vyjádřenou v litrech na 100 km bude auto mít, pokud uvažujeme účinnost motoru 25%? Připadá Vám celá tato situace reálná?
ID: 228;
Tags: výkon, t-vykon;
Autor: Marek Scholz (admin);
Position: 7/9;









