Vítejte! Tato stránka slouží jako databáze řešených fyzikálních úloh pro střední a základní školy.
▮
Vlastnosti ideálního plynu
#153,
Marek Scholz (admin),
pos:1/9,
kat
Určete, které z uvedených NEpatří mezi vlastnosti ideálního plynu:
a) dokonalá stlačitelnost; b) dokonalá průhlednost; c) nulová viskozita; d) nulová hustota a hmotnost.
Odpověď pisšte ve formě abcd
ID: 153;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Zahřátí plynu
#154,
Marek Scholz (admin),
pos:1/9,
kat
Pokud plyn zahřejeme, tak rychlost částic v průměru
Řešení:
Výsledek: vzroste
ID: 154;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Teplota plynu
#155,
Marek Scholz (admin),
pos:1/9,
kat
Teplota plynu je přímo úměrná
Řešení:
Výsledek: kinetické energii molekul
ID: 155;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Rychlost zvuku
#161,
Marek Scholz (admin),
pos:1/9,
kat
Rychlost zvuku ve vzduchu je ve srovnání se střední kvadrtickou rychlostí molekul dusíku
Řešení:
Výsledek: trochu menší
ID: 161;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Polohová potenciální energie
#162,
Marek Scholz (admin),
pos:1/9,
kat
Když se sloučí dva atomy kyslíku o dvouatomové molekuly O2, jak se změní polohová potenciální energie těchto atomů?
Řešení:
Výsledek: sníží se
ID: 162;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Kondenzace vody
#163,
Marek Scholz (admin),
pos:1/9,
kat
Když je v létě vlhký teplý vzduch a poté se v noci ochladí, tak plynná vodní pára kondenzuje do kapalné vody - tvoří se kapičky neboli rosa. Polohová potenciální energie molekul vody se při kondenzaci
ID: 163;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Kondenzace vody
#164,
Marek Scholz (admin),
pos:1/9,
kat
Když je v létě vlhký teplý vzduch a poté se v noci ochladí, tak plynná vodní pára kondenzuje do kapalné vody - tvoří se kapičky neboli rosa. Vyberte pravdivá tvrzení o procesu kondenzace:
a) Část potenciální polohová energie molekul se přemění na kinetickou energii molekul.
b) Potenciální polohová energie molekul ze zvýší.
c) Potenciální polohová energie molekul se sníží.
d) Proces kondenzace bude v podstatě exotermický.
Napište ve formě abcd
ID: 164;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Zvýšení tlaku
#165,
Marek Scholz (admin),
pos:1/9,
kat
Změní-li se teplota ideálního plynu za neměnného objemu z 20 °C na 40 °C, zvýší se tlak dvakrát, méně než dvakrát, nebo více než dvakrát?
Řešení: Je potřeba zjistit, kolikrát se zvětšila termodynamická teplota v Kelvinech. Ta vzrostla ze zhruba 293 K na 313 K. Teplota tak vzrostla jen o zhruba 7% a o tolik procent vzroste i tlak. Čili tlak vzroste mnohem méně než 2x.
Výsledek: méně než 2x
ID: 165;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Kreslení pV diagramu
#166,
Marek Scholz (admin),
pos:1/9,
kat
V nádobě s pístem jsou 2 litry plynu o tlaku 160 kPa. Píst je pohyblivý. Zakreslete do grafu (pV diagram), jak se bude měnit tlak plynu uvnitř nádoby v závislosti na objemu nádoby pod pístem, pokud teplota plynu zůstává stále stejná. Vyneste několik bodů grafu.
Řešení:
Výsledek: Grafem bude hyperbola - izoterma.
ID: 166;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Srovnej teploty v nádobách
#167,
Marek Scholz (admin),
pos:1/9,
kat
V jedné nádobě jsou 2 litry plynu o tlaku 160 kPa. V druhé nádobě je stejné množství plynu, ale plyn zaujímá objem 3 litry a má tlak 120 kPa. Rozhodněte, ve které nádobě má plyn vyšší teplotu.
Řešení: Podle stavové rovnice je teplota úměrná součinu tlaku a objemu, neboli $T \propto pV$.
Součin pV je vyšší ve druhé nádobě a je v ní tedy i vyšší teplota.
Výsledek: druhá nádoba
ID: 167;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Změny hustoty plynu
#170,
Marek Scholz (admin),
pos:1/9,
kat
Jak se mění hustota plynu v uzavřeném válci s pístem při
a) izobarickém zahřívání; b) izotermickém stlačování; c) izobarickém chlazení?
Řešení:
Výsledek: a) klesá; b) roste; c) nemění se
ID: 170;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Objem uniklého vzduchu
#168,
Marek Scholz (admin),
pos:1/9,
kat
Místnost má rozměr 5 x 3 x 4 metry a vzduch v ní má teplotu 7°C. Přišel zimomřivý Pepíček, zatěsnil dveře a okna, a zatopil tak, že teplota vzduchu vzrostla na 27°C. V okně je škvíra, takže se tlak nezměnil. Jaký objem vzduchu z místnosti uniknul?
Řešení: Můžeme to nahlédnout tak, že počítáme, o kolik se změní objem plynu při zahřátí během izobarického děje. Původní teplota je $T_1 = 280\,\mathrm{K}$ a objem je $V_1 = 60\,\mathrm{m^3}$.
Nová teplota je $T_2 = 300\,\mathrm{K}$ a objem $V_2$ chceme určit.
Objem je přímo úměrný teplotě. Teplota vzrostla poměrem 300/280 = 1,0714.
Tímto poměrem vzroste i objem, čili
$V_2 = 60\,\mathrm{m^3} \cdot 300/280 = 64,3\,\mathrm{m^3}$.
Změna objemu je tak 4,3 m$^3$.
Výsledek: 4,3 m3
Hint: Určete, kolikrát se zvýší termodynamická teplota plynu.
ID: 168;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Pojistný ventil
#169,
Marek Scholz (admin),
pos:1/9,
kat
Na uzavřené tlakové nádobě s plynem je pojistný ventil, který se otevírá při tlaku 0,25 MPa. Na počátku je teplota plynu v nádobě 20°C a tlak normální. Nádobu pak zahříváme nad plamenem. Při jaké teplotě plynu (°C) se ventil otevře?
Řešení: Počáteční tlak a teplota jsou 101 kPa, 293 K.
Koncový tlak je 250 kPa.
Jedná se o izochorický děj (neměnný objem) a tlak v nádobě je přímo úměrný teplotě.
Tlak má vzrůst poměrem 250/101 = 2,475.
Tímto poměrem musí vzrůst termodynamická teplota, čili ventil se otevře při teplotě
$T_2 = 293\,\mathrm{K} \cdot 250/101 = 725\,\mathrm{K}$.
To odpovídá teplotě 452°C.
Výsledek: 452 °C
Hint: Určete, kolikrát vzroste tlak. Nezapomeňte správě pracovat s termodynamickou teplotou a s převodem na °C.
ID: 169;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Počet stavových veličin
#173,
Marek Scholz (admin),
pos:1/9,
kat
Kolik stavových veličin musíme znát, abychom jednoznačně určili stav plynu o látkovém množství 1 mol?
ID: 173;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Rychlost hmotnějších molekul
#156,
Marek Scholz (admin),
pos:1/9,
kat
Vzduch je směsí několik různých plynů - dusíku, kyslíku, argonu, oxidu uhličitého... Vzduch má určitou teplotu a je v ustáleném rovnovážném stavu. Co jsou pak pravdivá tvrzení?
a) Všechny molekuly se pohybují téměř stejnou rychlostí; b) Molekuly s větší hmotností se pohybují pomaleji; c) Molekuly dusíku se pohybují obecně velice různými rychlostmi; d) Molekuly s větší hmotností mají v průměru větší kinetickou energii.
Odpověď pište ve formě abcd.
ID: 156;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Průměrná energie
#157,
Marek Scholz (admin),
pos:1/9,
kat
Mějme směs argonu a neonu sestávající z mnoha atomů těchto vzácných plynů. Průměrná kinetická energie připadající na jeden atom plynu je pak
Řešení: Jednoatomová molekula má tři stupně volnosti - tři translační stupně ve směrech x,y,z. Na každý stupeň volnosti připadá energie $\frac{1}{2}k_B T$. Čili průměrná energie jedné molekuly je pak
$E_1 = \frac{3}{2}k_B T$.
Výsledek: 3/2kT
ID: 157;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Grafy rozložení rychlostí
#158,
Marek Scholz (admin),
pos:1/9,
kat
Graf znázorňuje rozdělení rychlostí při stejné teplotě pro různé vzácné plyny: helium, xenon, argon, krypton. Která z křivek odpovídá heliu?
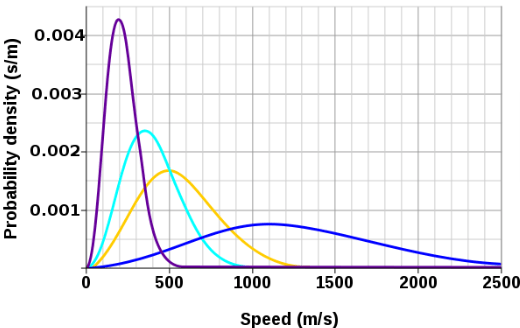
obr.
skrýt |
S |
M |
L
Řešení: Helium má z uvedených vzácných plynů nejnižší hmotnost, proto bude jeho střední kvadratická rychlost nejvyšší. Pak může být střední kinetická energie atomu helia stejná, jako kinetická energie těžších atomů.
Výsledek: modrá - nejširší
ID: 158;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Střední kvadratická rychlost
#159,
Marek Scholz (admin),
pos:1/9,
kat
Pokud budeme mít čtyři molekuly o rychlostech 100 m/s, 300 m/s, 300 m/s a 500 m/s, jaká bude střední kvadratická rychlost tohoto souboru?
Řešení:
Výsledek: 332 m/s
ID: 159;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Střední kvadratická rychlost vodíku
#160,
Marek Scholz (admin),
pos:1/9,
kat
Víme, že střední kvadratická rychlost molekuly N2 je při teplotě 300 K rovna 517 m/s. Atomu dusíku obsahuje 7 protonů a 7 neutronů. Dokážete na základě toho určit, jaká bude při stejné teplotě střední kvadratická rychlost molekuly H2?
Řešení: Atom dusíku je zhruba 14x těžší, než atom vodíku. V obou příkladech se jedná o dvouatomové plyny, čili poměr hmotnosti molekul je tentýž. Obě molekuly mají mít shodnou kinetickou energii ($1/2 mv^2). Menší hmotnost vodíku tak musí být kompenzována $\sqrt{14}\times$ větší rychlostí.
Výsledek: 517$\times\sqrt{14}$ m/s
ID: 160;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Objem bubliny
#171,
Marek Scholz (admin),
pos:1/9,
kat
Potápěči si musí dát pozor na to, aby stoupali k hladině pomalu a dělali si přestávky. Paradoxně musí být obzvlášt pomalý výstup v malých hloubkách blízko hladiny. Proč to tak je? Objasní to následující úloha: Jak se změní objem bubliny, která vystoupí o 10 m směrem nahoru, pokud se na začátku nachází v hloubce a) 40 m; b) 10 m? Děláte při výpočtu nějaké předpoklady?
Pro kontrolu zde vyplňte jen odpověď na otázku a), tedy o kolik procent se změní objem bubliny, když vystoupá o deset metrů z výšky 40 m. Teplotu považujte za konstantní.
Řešení: V hloubce 40 m je tlak součtem běžného atmosferického (101 kPa) a hydrostatického (400 kPa), čili $p_1$ = 501 kPa. O deset metrů výše je hydrostatický tlak o 100 kPa nižší, tedy $p_2$ = 401 kPa.
Okolní tlak klesl a objem bubliny tak stejným poměrem vzroste (bublina se rozepne), protože při konstantní teplotě se zachovává součin pV.
Nový objem je proto $V_2 = V_1 \cdot 501/401 = V_1 \cdot 1,25$.
Objem bubliny vzroste o 25%.
Při vystoupání z původní hloubky 10 m se tlak změní z 201 kPa na 101 kPa, tedy zhruba dvojnásobně klesne. Objem bubliny pak vzroste na dvojnásobek, čili o 100%.
Výsledek: 25 %
ID: 171;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Nadýchaný chleba
#172,
Marek Scholz (admin),
pos:1/9,
kat
Osvětlete procesy vedoucí k tomu, že chlena či jiné pečivo jsou krásně nadýchané, s velkými bublinami uvnitř.
Řešení:
Výsledek: Jednak činnost kvasnic - nárůst látkového množství plynu. Poté pečení - zvýšená teplota čili zvětšše
ID: 172;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Objem 5 g plynu
#175,
Marek Scholz (admin),
pos:1/9,
kat
V nádobě má být 5 g plynného kyslíku při tlaku 0,5 MPa. Jaký objem musí mít nádoba? Uveďte v litrech.
Řešení: Stavová rovnice říká, že $pV = nRT$.
Vyjádříme objem:
$V = nRT/p$
Známe $p$ a umíme dopočítat látkové množství:
$n = m/M_m$ = (5 g) / (32 g/mol) = 5/32 mol = 0,156 mol.
Teplota není uvedena, tedy předpokládáme pokojovou T = 293 K.
Dosadíme:
$V = (5/32 mol) \cdot (8,31) \cdot (293\,\mathrm{K}) / (5\times10^5\,\mathrm{Pa})$ = $7,6\times10^{-4}\,\mathrm{m^3}.
To je 0,76 litru, tedy zhruba jako lahev vína.
Výsledek: 0,76 litrů
ID: 175;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Molární objem plynu
#176,
Marek Scholz (admin),
pos:1/9,
kat
Jaký je objem jednoho molu plynu při běžné situaci ve vašem pokoji? Uveďte v litrech. Srovnejte s číslem, které možná znáte jako "molární objem plynu".
Řešení: Stavová rovnice říká, že $pV = nRT$.
Vyjádříme objem:
$V = nRT/p$
Známe $p \approx 100\,\mathrm{kPa}$ a $n = 1\,\mathrm{mol}$, pokojová teplota
T = 293 K.
Dosadíme:
$V = (1\,\mathrm{mol}) \cdot (8,31) \cdot (293\,\mathrm{K}) / (1\times10^5\,\mathrm{Pa})$ = $24,3\times10^{-3}\,\mathrm{m^3}$.
To je 24,3 litru. Ze školy většinou známe molární objem plynu 22,4 litrů. Ten ale platí za "normálních podmínek", to jest tlak ca. 101 kPa, ale hlavně pozor: teplota 0°C.
Výsledek: 24,3 litrů
ID: 176;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Zvýšení teploty a objemu
#177,
Marek Scholz (admin),
pos:1/9,
kat
Teplota plynu ve válci byla zvýšena ze 20°C na 200°C a objem plynu se přitom zvýšil o 1/3. Jak se změnil tlak plynu? Změnu vyjádřete v procentech.
Řešení: Platí $T_1$ = 293 K; $T_2$ = 473 K;
pro objemy máme $V_1/V_2 = \frac{3}{4}$.
Můžeme si tedy klidně říci, že původní objem má hodnotu 1 a nový objem hodnotu 4/3.
Látkové množství plynu se nemění a proto platí
$p_1V_1/T_1 = p_2V_2/T_2$.
Zajímá nás, jaký je vztah mezi $p_2$ a $p_1$, čili podíl $p_2/p_1$. Ten vyjádříme:
$\frac{V_1}{V_2} \cdot \frac{T_2}{T_1} = \frac{p_2}{p_1}$.
Dosadíme
$\frac{p_2}{p_1} = \frac{3}{4} \cdot \frac{473}{293} = 1,21 $.
Čili došlo k nárůstu tlaku o 21 %.
Výsledek: 21 %
Hint: Užijte poznatek, že výraz pV/T se zachovává. Nový objem vyjádřete jako násobek toho původního.
ID: 177;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Výška výstupu balonu
#174,
Marek Scholz (admin),
pos:1/9,
kat
Může horkovzdušný balon vystoupat od hladiny moře až k vrcholu Mt. Everestu, pokud textilie balonu vydrží teplotu do 120°C? Diskutujte. Typický balon má objem 2800 m3 a konstrukce s palivem má hmotnost okolo 400 kg.
ID: 174;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Stavová rovnice pro hustotu
#178,
Marek Scholz (admin),
pos:1/9,
kat
Vyjádřete vztah mezi hustotou plynu a stavovými veličinami + molární hmotností plynu. Vyjděte z definice hustoty, stavové rovnice a definice molární hmotnosti.
Řešení: Máme vztahy $pV = nRT$; $n = m/M_m$, $\rho = m/V$.
Postup 1:
Ve stavové rovnici látkové množství nahradíme z druhého vztahu:
$pV = mRT/M_m$.
Vztah přeuspořádáme tak, abychom měli výraz $m/V$:
$p = \frac{mRT}{V M_m} = \frac{\rho RT}{M_m}$.
To je již hledaný vztah, ze kterého bychom samozřejmě mohli vyjádřit hustotu.
Postup 2:
Vyjdeme ze vztahu $\rho = m/V$. Hmotnost nahradíme výrazem $m = nM_m$:
$\rho = nM_m/V$.
Stavovou rovnici napíšeme jako
$p = nRT/V$.
Vidíme, že platí $n/V = \frac{p}{RT}$
Dosadíme do vztahu pro hustotu:
$\rho = nM_m/V = \frac{p}{RT} \cdot M_m$.
Výsledek: $\rho = \frac{p M_m}{RT}$
ID: 178;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
