Vítejte! Tato stránka slouží jako databáze řešených fyzikálních úloh pro střední a základní školy.
▮
Deska v bahně
#241,
Marek Scholz (admin),
pos:2/9,
kat
Pan Vrták váží 120 kg a má doma dvě dřevěné desky. První má rozměr 2m x 1,2m a druhá má rozměr 1m x 1,6m. Desky dal do bahna. Nejdřív si stoupl na první desku a potom na druhou desku. Ve kterém případě se deska víc proboří do bahna?
Řešení: Druhá deska má menší plochu. Tíha pana Vrtáka se rozloží do menší plochy a tlak pod druhou deskou tak bude větší.
Výsledek: Druhá deska má menší plochu. Tíha pana Vrtáka se rozloží do menší plochy a tlak pod druhou deskou ta
ID: 241;
Tags: ;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Tlak na desku v bahně
#242,
Marek Scholz (admin),
pos:2/9,
kat
Pan Vrták váží 120 kg a má doma dvě dřevěné desky. První má rozměr 2m x 1,2m a druhá má rozměr 1m x 1,6m. Desky dal do bahna. Nejdřív si stoupl na první desku. Jakým tlakem deska působí na zem? Vyjádřete v Pa, uvažujte g = 10 m/s2.
Řešení: $F = mg$ = 1200 N. $S = 2,4\,\mathrm{m^2}$.
$p = F/S = (1200\,\mathrm{N}) / (2,4\,\mathrm{m^2})$ $= 500\,\mathrm{N/m^2} = 500\,\mathrm{Pa}$
Deska působí na zem tlakem 500 Pa.
Výsledek: 500 Pa
ID: 242;
Tags: ;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Pascal versus N/cm2
#246,
Marek Scholz (admin),
pos:3/9,
kat
Na podlaze máte desku ve tvaru čtverce o straně 1 m. Představte si, že na každý jeden čtvereček o ploše 1cm2 působí síla o velikosti 1 N.
a) Jak velká síla působí dohromady na celou desku?
b) Jak velkým tlakem (v Pascalech) působí deska na podlahu?
Odpovězte na otázku b)
Řešení:
Výsledek: 10000 Pa
ID: 246;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
kilopascal versus N/cm2
#247,
Marek Scholz (admin),
pos:3/9,
kat
Píst působí na kapalinu tlakem 2 N/cm2. a) Kolik je to pascalů? b) Kolik je to kilopascalů?
Odpovězte na otázku b)
ID: 247;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Píst stříkačky
#248,
Marek Scholz (admin),
pos:3/9,
kat
Edudant si vzal velkou injekční stříkačku, naplnil vodou a zacpal výstupní otvor. Potom stlačil píst silou o velikosti 30 N. Píst má plochu 5 cm2. Jak velký tlak vyvolává píst na vodu ve stříkačce? Vyjádřete v kPa.
Řešení: p = F/S.
Pokud bychom dosadili plochu v cm2, tak dostaneme tlak
p = 30 N / 5 cm2 = 6 N/cm2
To však nejsou pascaly, protože Pascal je to samé jako N/m2.
Do 1 m2 se vejde 10000 cm2.
Když na 1 cm2 připadá síla 6 N, tak na 1 m2 bude připadat síla 60000 N.
Tlak je tedy 60000 N/m2 = 60000 Pa = 60 kPa.
Samozřejmě můžeme plochu také vyjádřit jako S = 5 cm2 = 0,0005 m2 a počítat
p = 30 N / 0,0005 m2 = 60000 N/cm2.
Výsledek: 60 kPa
ID: 248;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Tlak pod trifidem
#251,
Marek Scholz (admin),
pos:3/9,
kat
Třínohá obluda trifid má zrovna jednu nohu zvednutou a váhu rozvnoměrně rozloženou mezi zbývající nohy. V takovém případě chodidlo způsobuje tlak 18 kPa. Poté trifid dá nohu zpět na zem a opět váhu rovnoměrně rozloží. Jaký tlak potom budou způsobovat chodidla na zem?
Určete v jednotce kPa.
Řešení: Poté, co dá nohu na zem, se bude tíha trifida rozkládat na 3 nohy namísto původních 2 nohou. Plocha vzroste poměrem 3/2 = 1,5. Tlak je nepřímo úměrný ploše a tedy tlak klesne 1,5 x.
Výsledný tlak tedy je
18 kPa / 1,5 = 18 kPa * 2/3 = 12 kPa.
Výsledek: 12 kPa
ID: 251;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Dveře ponorky
#253,
Marek Scholz (admin),
pos:4/9,
kat
Dveře ponorky mají tvar obdélníku o stranách 2 m x 80 cm. Jak velká síla na ně působí, když pod hladinou na dveře působí tlak o velikosti 50 kPa?
Řešení: Plocha dveří je S = 2m x 0,8m = 1,6 m$^2$.
Sílu na dveře určíme jako
$F = p \cdot S$
Dosadíme
$F = p \cdot S$ = (50000 Pa) * (1,6 m$^2$) = 80000 N.
To je hodně - odpovídá to tíze osmi tun!
Výsledek: 80000 N
ID: 253;
Tags: ;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Moment klíče
#99,
Marek Scholz (admin),
pos:2/9,
kat
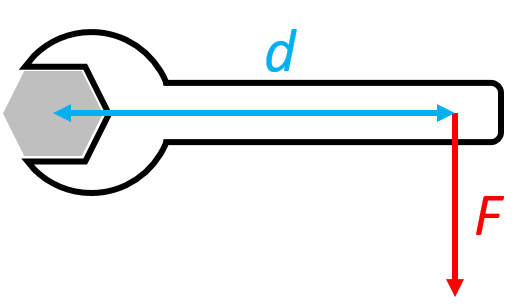
Určete, jakou velikost má moment síly, který utahuje šroub, když síla o velikosti 160 N působí ve vzdálenosti 25 cm od osy šroubu.
obr.
skrýt |
S |
M |
L
Řešení: Moment síly (schopnost síly něčím otáčet) závisí jednak na velikosti síly $F$ a jednak na délce ramene síly $d$. V našem případě pro moment síly platí:
$M = F \cdot d$.
Pokud nepřevedeme cm na metry, tak máme
$M = 160\,\mathrm{N} \cdot 25\,\mathrm{cm} = 4000\,\mathrm{N \cdot cm}$.
Pokud ale budeme chtít mít výsledek v základní jednotce, čili N.m, musíme převést:
25 cm = 0,5 m = 1/4 m.
Dosadíme:
$M = 160\,\mathrm{N} \cdot \frac{1}{4}\,\mathrm{m} = 40\,\mathrm{N \cdot m}$.
Výsledný moment síly je 40 N.m.
Výsledek: 40 N.m
Hint: Schopnost síly něčím otáčet závisí jednak na velikosti síly a jednak na délce jejího ramene. Z toho plyne vztah pro moment síly, který si jistě uvědomíte. Pak také nezapomeňte na převod jednotek.
ID: 99;
Tags: ;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Moment utahování
#100,
Marek Scholz (admin),
pos:2/9,
kat
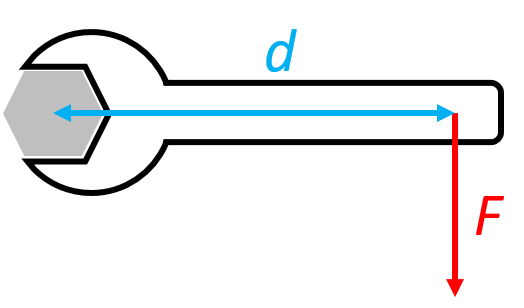
Gertruda píchnula a potřebuje vyměnit kolo. Přečetla si, že by šrouby na disku měla utáhnout momentem o velikosti 120 N.m. Jakou silou musí působit klíč, který má délku 40 cm? Může to Gertruda vůbec zvládnout?
obr.
skrýt |
S |
M |
L
Řešení: Moment síly (schopnost síly něčím otáčet) závisí jednak na velikosti síly $F$ a jednak na délce ramene síly $d$. Pro moment síly platí:
$M = F \cdot d$.
Ze zadání víme, že $M = 120\,\mathrm{Nm}$ a $d = 40\,\mathrm{cm} = 0,4\,\mathrm{m}$.
Hledáme velikost síly $F$. Dosadíme do vztahu pro moment síly:
$120\,\mathrm{Nm} = F \cdot 0,4\,\mathrm{m}$.
Obě strany vydělíme 0,4 a dostaneme:
$F = 120 / 0,4 = 1200 / 4 = 300 \,\mathrm{N}$.
Tedy musíme působit silou o velikosti 300 N.
To je jako zvedat 30 kg. Tedy člověkem zvádnutelné, ale obtížné.
Výsledek: 300 N
Hint: Napište si vztah pro moment síly a dosaďte známé hodnoty. Velikost síly bude neznámá, kterou dopočítáte z rovnice. Nezpomeňte na převod na základní jednotky.
ID: 100;
Tags: ;
Autor: Marek Scholz (admin);
Position: 2/9;
▮
Nejlepší klíč
#101,
Marek Scholz (admin),
pos:1/9,
kat
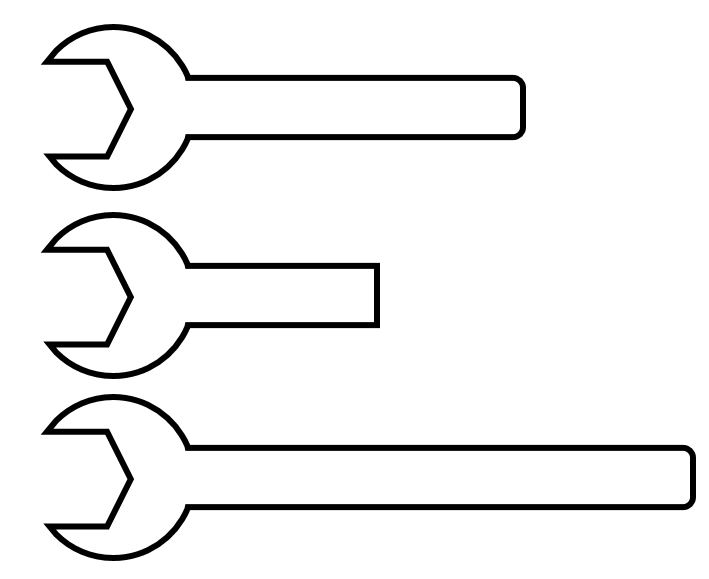
Kterým z klíčů se mi nejlépe podaří povolit zatuhlý šroub?
obr.
skrýt |
S |
M |
L
Řešení: Nejlépe to půjde nejdelším klíčem, protože pak síla naší ruky bude působit nejdále od osy otáčení a síla tak bude mít nejdelší rameno. Můžeme také říci, že máme dlouhou "páku".
Výsledek: dole
ID: 101;
Tags: ;
Autor: Marek Scholz (admin);
Position: 1/9;
▮
Houpačka
#105,
Marek Scholz (admin),
pos:3/9,
kat
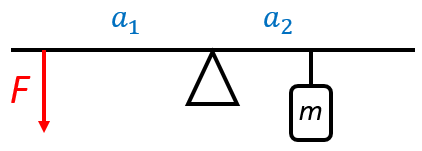
Na houpačce je zavěšeno závaží o hmotnosti 8 kg ve vzdálenosti 120 cm. Na druhé straně houpačky působíme rukou silou a udržujeme houpačku v rovnováze. Rozhodněte bez počítání o velikosti síly ruky.
obr.
skrýt |
S |
M |
L
Řešení: Podle obrázku má síla od ruky delší rameno než síla od tíhy závaží, a tedy síla od ruky bude stačit menší, než kolik je tíha závaží.
Výsledek: je menší než 80 N
ID: 105;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Houpačka
#106,
Marek Scholz (admin),
pos:3/9,
kat
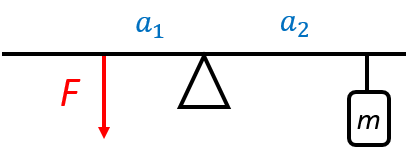
Na houpačce je zavěšeno závaží o hmotnosti 20 kg ve vzdálenosti 100 cm. Na druhé straně houpačky působíme rukou silou a udržujeme houpačku v rovnováze. Rozhodněte bez počítání o velikosti síly ruky
obr.
skrýt |
S |
M |
L
Řešení: Podle obrázku má síla od ruky kratší rameno než síla od tíhy závaží, a tedy síla od ruky musí být větší, než kolik je tíha závaží.
Výsledek: je větší než 200 N
ID: 106;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Kolik váží
#129,
Marek Scholz (admin),
pos:3/9,
kat
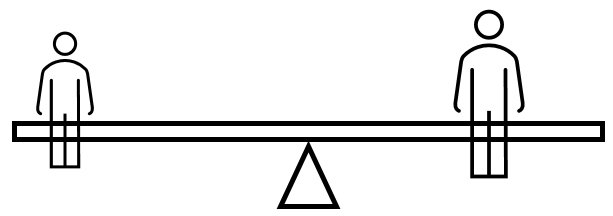
Pepek námořník a Božena Němcová si sednuli na kládu podepřenou uprostřed. Pepek má hmotnost 90 kg a sednul si 200 cm od středu klády. Když si Božena sednula 250 cm od středu, tak byla s Pepkem v rovnováze. Jaká je hmotnost slovutné Boženy?
obr.
skrýt |
S |
M |
L
Řešení: Aby byla houpačka v rovnováze (v klidu), musí být schopnost Boženy a schopnost Pepka otáčet tyčí stejná. To fyzikálně vyjádříme tak, že má nastat rovnováha momentů sil na obou stranách houpačky. Tedy moment tíhové síly od Pepka musí být stejně velký jako moment tíhové síly od Boženy. To vyjádříme rovnicí:
$M_p = M_b$
neboli
$F_p \cdot d_p = F_b \cdot d_b$
a dosadíme známé hodnoty
$900\,\mathrm{N} \cdot 2\,\mathrm{m} = F_b \cdot 2,5\,\mathrm{m}$
osamostatníme tíhu Boženy $F_b$ tak, že obě strany rovnice vydělíme 2,5 m:
$900\,\mathrm{N} \cdot 2/2,5 = F_b$
Když se zamyslíme, tak zjistíme, že podíl 2/2,5 odpovídá zlomku $\frac{4}{5}$. Výsledek proto
$F_b = 900\,\mathrm{N} \cdot \frac{4}{5} = 720\,\mathrm{N}$.
Tíha 720 N odpovídá hmotnosti Boženy 72 kg.
Mohli bychom sazmořejmě rovnou také řešit rovnici
$m_p \cdot d_p = m_b \cdot d_b$
a dosadit
$90 \cdot 2 = m_b \cdot 2,5$
a zase stejně osamostatnit $m_b = 90 \cdot 2/2,5 = 90 \cdot \frac{4}{5}$ = 72 kg.
Výsledek: 72 kg
Hint: Aby byla houpačka v rovnováze (v klidu), musí být schopnost Boženy a schopnost Pepka otáčet tyčí stejná. To fyzikálně vyjádříme tak, že má nastat rovnováha momentů sil na obou stranách houpačky. Tedy moment tíhové síly od Pepka musí být stejně velký jako moment tíhové síly od Boženy: $M_p = M_b$
neboli $F_p \cdot d_p = F_b \cdot d_b$.
ID: 129;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Tlak nohou
#240,
Marek Scholz (admin),
pos:3/9,
kat
Experimentální úloha: Co nejpřesněji určete, jakým tlakem působíte na podlahu, pokud si stoupnete v pantoflích a) na obě nohy, b) na jednu nohu.
ID: 240;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Tlak od cihly
#243,
Marek Scholz (admin),
pos:3/9,
kat
Paní Zděna má doma velkou cihlu ve tvaru kvádru o rozměrech 20 x 30 x 15 cm. Cihla má hmotnost 18 kg. Chce ji postavit na podlahu na některou ze stěn tak, aby cihla působila co největším tlakem. Jak velký pak bude tlak, kterým cihla na podlahu působí? Uvažujte g = 10 m/s2.
Řešení: Aby cihla půsila maximálním tlakem, musí stát na své nejmenší stěně. Nejmenší stěna má plochu 20cm x 15cm = 300 cm2 = 0,03 m2. Tlak potom je
$p = F/S$ = 180 N / 0,03 m2 = 6000 N/m2 = 6000 Pa.
Výsledek: 6000 Pa
ID: 243;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Krabice na ledě
#245,
Marek Scholz (admin),
pos:4/9,
kat
Tenký led vydrží tlak maximálně 3 kPa. Paní Zbořená chce na led dát krabici s dnem o rozměru 40 cm x 50 cm a naložit do ni lahvičky s marmeládou. Jakou maximální hmotnost může do krabice naložit, aby se led neprobořil?
Uvažujte g = 10 m/s2.
Řešení: Plocha dna je 40 cm x 50 cm = 2000 cm2 = 0,2 m2.
Tlak $p = F/S$.
Maximální síla tak má velikost
$F = p \cdot S$ = 3000 Pa * 0,2 m2 = 600 N.
To odpovídá nákladu o hmotnosti asi 60 kg.
Výsledek: 60 kg
ID: 245;
Tags: ;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Špunt v sudu
#249,
Marek Scholz (admin),
pos:4/9,
kat
Rákosníček má doma sud. U dna sudu je špunt o ploše 8 cm2 a voda vyvolává tlak o velikosti 8 kPa. Jak velká síla působí na špunt?
Řešení: Plochu špuntu musíme vyjádřit v základní jednotce, tedy m2.
Jeden cm2 je desetitisícina metru čtverečného, tedy plochu můžeme napsat jako
S = 8 cm2 = 8/10000 m2
Síla na špunt bude
$F = p \cdot S$ = (8000 Pa) * (8/10000 m2) = 6,4 N.
Síla na špunt bude 6,4 N.
Výsledek: 6,4 N
ID: 249;
Tags: ;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Sloní noha
#250,
Marek Scholz (admin),
pos:3/9,
kat
Slon Jumboš stojí rovnoměrně na všech čtyřech nohách, přičemž každá noha na zem působí tlakem 6 kPa. Jak velkým tlakem bude působit každá noha, když jednu nohu zvedne a váhu opět roznese rovnoměrně?
Určete v jednotce kPa.
Řešení: Čím větší bude plocha, na kterou slon váhu rozloží, tím menší bude tlak, a čím menší bude plocha, tím větší bude tlak. Kdyby místo čtyřech nohou stoupnul jen na jednu, tak by tlak způsobený nohou byl 4x větší, čili 24 kPa. Když pak roznese váhu na 3 nohy, tak výsledkný tlak pod každou nohou bude 24 kPa / 3 = 8 kPa.
Výsledek: 8 kPa
ID: 250;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Tlak krychlové krabice
#252,
Marek Scholz (admin),
pos:3/9,
kat
Na stole leží krabice o hmotnosti 20 kg a má tvar krychle se stranou délky 40 cm. Jak velký tlak kvádr na stůl vyvolává? (Uvažujte g = 10 m/s2)
Řešení: Krabice stojí na čtvercové stěně o ploše S = 0,4m x 0,4m = 0,16 m$^2$.
Tíha krabice je 200 N.
Tlak vypočteme jako
p = F/S
Dosadíme
p = F/S = (200 N) / (0,16 m$^2$) = 200/16 * 100 = 1250 Pa.
Výsledek: 1250 Pa
ID: 252;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Houpačka
#102,
Marek Scholz (admin),
pos:3/9,
kat
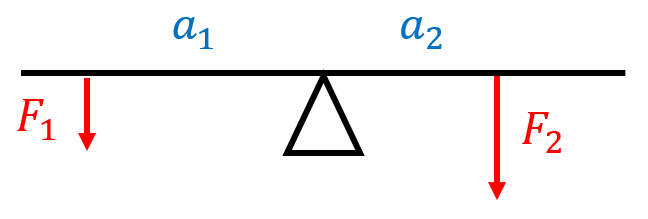
Na houpačku působí dvě síly, každá na jedné straně od osy otáčení. Větší síla má velikost 240 N a působí ve vzdálenosti 2 metry od osy otáčení. Menší síla má velikost 80 N. V jaké vzdálenosti od osy otáčení musí působit, aby byla houpačka v rovnováze?
obr.
skrýt |
S |
M |
L
Řešení: Řešíme rovnováhu momentů sil na obou stranách houpačky, čili má platit $M_1 = M_2$. Moment síly závisí na velikosti síly a délce jejího ramene, čili rovnováhu vyjádříme jako rovnost
$F_1 \cdot a_1 = F_2 \cdot a_2$.
Všimněte si, někdy délku ramena značíme jako $d$, někdy jako $a$ - na tom nesejde.
Dosadíme známé hodnoty:
$240\,\mathrm{N} \cdot 2\,\mathrm{m} = 80\,\mathrm{N} \cdot a_2$.
Neznámou je délka ramene $a_2$. Tu chceme osamostatnit. Obě strany rovnice proto vydělíme 80 N:
$\frac{240\,\mathrm{N} \cdot 2\,\mathrm{m}}{80\,\mathrm{N}} = a_2$.
Výsledek je zjevně 6 m.
Menší síla je 3x menší a musí proto mít trojnásobné rameno než větší síla.
Výsledek: 6 m
ID: 102;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Houpačka
#103,
Marek Scholz (admin),
pos:3/9,
kat
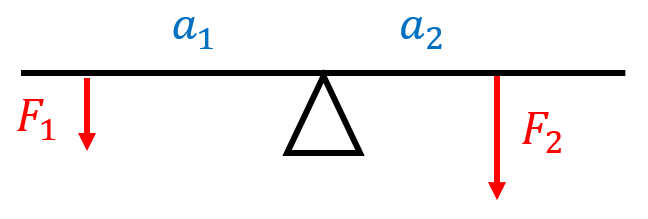
Na houpačku působí dvě síly, každá na jedné straně od osy otáčení. Menší síla má velikost 120 N a působí ve vzdálenosti 2 metry od osy otáčení. Větší síla má velikost 160 N. V jaké vzdálenosti od osy otáčení musí působit větší síla, aby byla houpačka v rovnováze?
obr.
skrýt |
S |
M |
L
Řešení: Řešíme rovnováhu momentů sil na obou stranách houpačky:
$F_1 \cdot a_1 = F_2 \cdot a_2$.
Dosadíme známé hodnoty:
$120\,\mathrm{N} \cdot 2\,\mathrm{m} = 160\,\mathrm{N} \cdot a_2$.
Neznámou je délka ramene $a_2$. Tu chceme osamostatnit. Obě strany rovnice proto vydělíme 160 N:
$\frac{120\,\mathrm{N} \cdot 2\,\mathrm{m}}{160\,\mathrm{N}} = a_2$.
Výsledek je zjevně 1,5 m. (Protože 240/160 = 24/16 = 3/2)
Větší síla má kratiší rameno, a sice o délce 1,5 m.
Výsledek: 1,5 m
ID: 103;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Houpačka
#104,
Marek Scholz (admin),
pos:3/9,
kat
Na houpačku působí dvě síly, každá na jedné straně od osy otáčení. Menší síla má velikost 360 N a působí ve vzdálenosti 300 cm od osy otáčení. Větší síla působí ve vzdálenosti 180 cm od osy otáčení. Jakou velikost musí mít větší síla, aby byla houpačka v rovnováze?
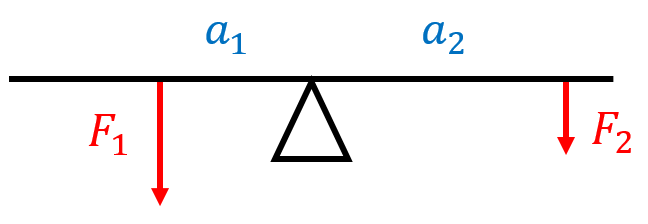
obr.
skrýt |
S |
M |
L
Řešení: Řešíme rovnováhu momentů sil na obou stranách houpačky:
$F_1 \cdot a_1 = F_2 \cdot a_2$.
Dosadíme známé hodnoty:
$360\,\mathrm{N} \cdot 3\,\mathrm{m} = F_2 \cdot 1,8\,\mathrm{m}$.
Neznámou je velikost síly $F_2$. Tu chceme osamostatnit. Obě strany rovnice proto vydělíme 1,8 m:
$\frac{360\,\mathrm{N} \cdot 3\,\mathrm{m}}{1,8\,\mathrm{m}} = F_2$.
Nyní se vyplatí počítat chytře:
$360\cdot3/1,8 = 360\cdot30/18$ = $360/18\cdot30 = 20\cdot30 = 600$.
Větší síla má tedy velikost 600 N.
Výsledek: 600 N
ID: 104;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Hooupačka
#107,
Marek Scholz (admin),
pos:3/9,
kat
Na houpačce je zavěšeno závaží o hmotnosti 24 kg ve vzdálenosti 90 cm od osy otáčení. Na druhé straně houpačky působíme rukou silou ve vzdálenosti 135 cm od osy otáčení a udržujeme houpačku v rovnováze. Velikost síly od ruky musí být
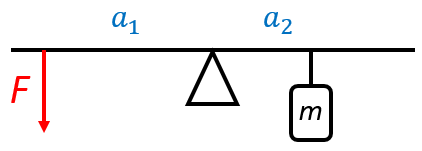
obr.
skrýt |
S |
M |
L
Řešení: Řešíme rovnováhu momentů sil na obou stranách houpačky:
$F_1 \cdot a_1 = F_2 \cdot a_2$.
Síla od závaží je 240 N.
Všimneme si, že délky ramen nejsou náhodná čísla: 135 cm = 90 cm + 45 cm, čili rameno síly ruky je 1,5x delší než rameno tíhy závaží!
Síla od ruky tak bude 1,5x menší než tíha závaží, neboli
F = 240 N / 1,5
Dělit 1,5 je stejné jako dělit zlomkem 3/2 a to je stejné jako násobit zlomkem 2/3. Máme tak
$F = 240\,\mathrm{N} \cdot \frac{2}{3} = 160 \,\mathrm{N} $
Síla od ruky musí mít velikost 160 N.
Výsledek: 160 N
ID: 107;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Houpačka
#108,
Marek Scholz (admin),
pos:3/9,
kat
Na houpačce je zavěšeno závaží o hmotnosti 36 kg ve vzdálenosti 90 cm od osy otáčení. Na druhé straně houpačky působíme rukou silou o velikosti 300 N. V jaké vzdálenosti od osy otáčení ruka musí působit?
Řešení: Řešíme rovnováhu momentů sil na obou stranách houpačky:
$F_1 \cdot d_1 = F_2 \cdot d_2$.
Síla od závaží je 360 N. Dosadíme známé hodnoty, délku klidně v cm (pak nám výsledek taky vyjde v cm):
$360\,\mathrm{N} \cdot 90\,\mathrm{cm} = 300\,\mathrm{N} \cdot d_2$.
Neznámou je délka ramene $d_2$. Tu chceme osamostatnit. Obě strany rovnice proto vydělíme 300 N:
$\frac{360\,\mathrm{N} \cdot 90\,\mathrm{cm}}{300\,\mathrm{N}} = d_2$.
Tedy
$d_2 = 360\cdot90/300 = 36\cdot9/3$ = $36\cdot3 = 108\,\mathrm{cm}$
Ruka musí působit ve vzdálenosti 1,08 m od osy, čili 108 cm.
Výsledek: 108 cm
ID: 108;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Páka
#109,
Marek Scholz (admin),
pos:3/9,
kat
Vařbuřt zvedá pytel o hmotnosti 15 kg, který je zavěšený na tyči. Jak velkou silou je potřeba působit na konci tyče o celkové délce 150 cm, abychom tyč udrželi v rovnováze? Vzdálenost pytle od osy otáčení je 80 cm.
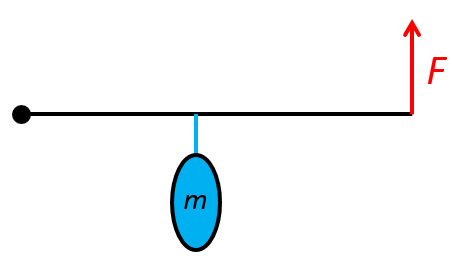
obr.
skrýt |
S |
M |
L
Řešení: Řešíme rovnováhu momentů sil:
$F_1 \cdot d_1 = F_2 \cdot d_2$.
Síla od závaží je 150 N. Dosadíme známé hodnoty, délku klidně v cm (pak nám výsledek taky vyjde v cm):
$150\,\mathrm{N} \cdot 80\,\mathrm{cm} = F_2 \cdot 150\,\mathrm{cm}$.
Neznámou je velikost síly $F_2$. Tu chceme osamostatnit. Obě strany rovnice proto vydělíme 150 cm:
$\frac{150\,\mathrm{N} \cdot 80\,\mathrm{cm}}{150\,\mathrm{cm}} = F_2$.
Čísla 150 se nám hezky pokrátí a výsledek je $F_2 = 80\,\mathrm{N}$.
Výsledek: 80 N
ID: 109;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Páka
#110,
Marek Scholz (admin),
pos:3/9,
kat
Princezna Fakana zvedá pytel o hmotnosti 40 kg, který je zavěšený na tyči. Jak velkou silou musí působit na konci tyče? Vyznačené vzdálenosti jsou a = 50 cm, b = 90 cm.
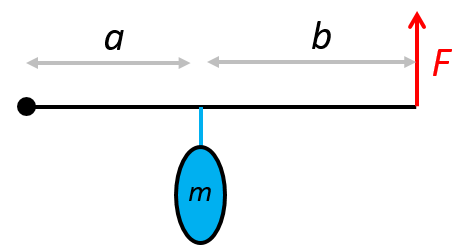
obr.
skrýt |
S |
M |
L
Řešení: Pytel má tíhu $F_1 = 400 \,\mathrm{N}$ a tato síla má délku ramena $d_1 = a = 50\,\mathrm{cm}$.
Pozor ale, síla od ruky $F_2$, jejíž velikost hledáme, má délku ramena $d_2 = a + b = 140\,\mathrm{cm}$!
Nyní již stačí dosadit
$F_1 \cdot d_1 = F_2 \cdot d_2$.
$400\,\mathrm{N} \cdot 50\,\mathrm{cm} = F_2 \cdot 140\,\mathrm{cm}$.
Neznámou je velikost síly $F_2$. Tu chceme osamostatnit. Obě strany rovnice proto vydělíme 140 cm:
$\frac{400\,\mathrm{N} \cdot 50\,\mathrm{cm}}{140\,\mathrm{cm}} = F_2$.
Můžeme počítat $400\cdot50/140 = 400\cdot5/14$ = $2000/14 \approx 142\,\mathrm{N}$.
Fakana musí působit silou o velikosti 142 N.
Výsledek: 142 N
Hint: Pozor, musíte si správně uvědomit, co je délka ramena síly od ruky.
ID: 110;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Kde podepřít
#111,
Marek Scholz (admin),
pos:4/9,
kat
Na koncích tyčky jsou zavěšena závaží o hmotnostech 1 kg a 2 kg. Tyčka je rozdělena na 12 kousků. Pod kterou značkou musíme tyčku podepřít, aby byla v rovnováze? (Samotná tyčka je velmi lehká a její hmotnost zanedbáváme).
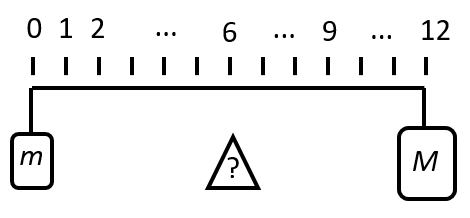
obr.
skrýt |
S |
M |
L
Řešení: Menší závaží musí mít 2x delší rameno. 2 díly délky tyčky tak připadnou k menšímu závaží a 1 díl k většímu závaží. Délku tyčky tak dělíme na 3 díly. Každý díl má 4 kousky. K menšímu závaží připadnou 2 díly, čili 8 kousků.
Výsledek: 8
Hint: Místo opření musí být blíž k těžšímu závaží, aby mělo kratší rameno. Opření musí být dvakrát blíž k těžšímu než k lehčímu...Tyčku vlastně dělíme v poměru 1:2.
ID: 111;
Tags: ;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Kde podepřít
#112,
Marek Scholz (admin),
pos:4/9,
kat
Na koncích tyčky jsou zavěšena závaží o hmotnostech 15 kg a 5 kg. Tyčka je rozdělena na 12 kousků. Pod kterou značkou musíme tyčku podepřít, aby byla v rovnováze? (Samotná tyčka je velmi lehká a její hmotnost zanedbáváme).
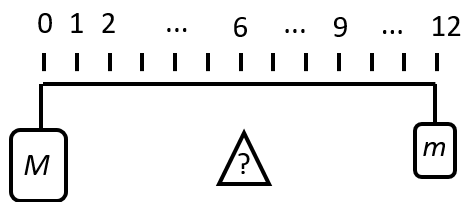
obr.
skrýt |
S |
M |
L
Řešení: Menší závaží je 3x lehčí a musí mít 3x delší rameno. 3 díly délky tyčky tak připadnou k menšímu závaží a 1 díl k většímu závaží. Délku tyčky tak dělíme na 4 díly. Každý díl má tak 3 kousky. K většímu závaží připadne 1 díl, čili 3 kousky.
Výsledek: 3
Hint: Těžké závaží je 3x těžší. Místo opření musí být blíž k těžšímu závaží, aby mělo kratší rameno. Tyčku tak vlastně musíme rozdělit v poměru 1:...
ID: 112;
Tags: ;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Kde podepřít
#113,
Marek Scholz (admin),
pos:4/9,
kat
Na koncích tyčky jsou zavěšena závaží o hmotnostech 2 kg a 3 kg. Tyčka má celkovou délku 75 cm. V jaké vzdálenosti od těžšího závaží musíme tyčku podepřít, aby byla v rovnováze? (Samotná tyčka je velmi lehká a její hmotnost zanedbáváme).

obr.
skrýt |
S |
M |
L
Řešení: Představme si, že nejdřív chceme rozdělit 75 kč mezi dvojici a trojici kamarádů. To je dohromady 5 lidí a na každého má připadnout 75 kč / 5 = 15 kč. Dvojici tak dáme 2 x 15 kč = 30 kč a trojici 3 x 15 kč = 45 kč. Tím jsme vlastně číslo 75 rozdělili v poměru 2:3. Výsledek dělení je 30 a 45.
Pro rozdělení tyčky, aby nastala rovnováha momentů sil, je to podobné. Akorát ale menší závaží musí dostat větší část tyčky a větší závaží menší část tyčky.
Na 3 kg závaží tak připadne 30 cm tyčky.
Výsledek: 30 cm
Hint: Tyčku musíme rozdělit v poměru 3:2. Místo opření ale musí být blíže k těžšímu závaží.
ID: 113;
Tags: ;
Autor: Marek Scholz (admin);
Position: 4/9;
▮
Houpačka
#127,
Marek Scholz (admin),
pos:3/9,
kat
Houpačka (dlouhá kláda o délce 6 m) je podepřena uprostřed. Dva kamarádi Ariela a Bluto se chtějí kvalitně pohoupat, tedy sednout si tak, aby houpačka byla v rovnováze. Ariela má hmotnost 50 kg a sedla si 40 cm od okraje. Bluto má hmotnost 65 kg. Jak daleko od okraje klády si musí sednout? Určete v centimetrech.
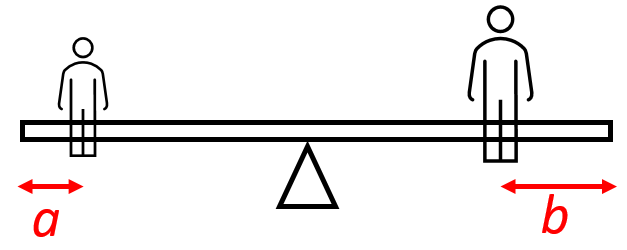
obr.
skrýt |
S |
M |
L
Řešení: Musíme si správně uvědomit délky ramen sil, čili v tomto případě vzdálenost působiště sil od osy otáčení. Kláda má celkovou délku 6 m a na každou stranu tak připadá 300 cm.
Ariela proto sedí 240 cm od středu (osa otáčení).
Nyní již stačí dosadit do rovnosti
$m_A \cdot d_A = m_B \cdot d_B$.
$50\,\mathrm{kg} \cdot 240\,\mathrm{cm} = 65\,\mathrm{kg} \cdot d_B$.
Neznámou je vzdálenost Bluta od středu $d_B$. Tu chceme osamostatnit. Obě strany rovnice proto vydělíme 65 kg:
$\frac{50\,\mathrm{kg} \cdot 240\,\mathrm{cm}}{65\,\mathrm{kg}} = d_B$.
Můžeme počítat $50\cdot240/65 = 10\cdot240/13$ a dostaneme $d_b \approx 185\,\mathrm{cm}$.
To je Blutova vzdálenost od středu houpačky, avšak ptáme se na vzdálenost od okraje.
Ta je pak zřejmě 300 cm - 185 cm = 115 cm.
Výsledek: 115 cm
Hint: Pozor, jsou v zadání se mluví o vzdálenosti od okraje tyče, ale to není to samé jako rameno síly vůči ose otáčení.
ID: 127;
Tags: ;
Autor: Marek Scholz (admin);
Position: 3/9;
▮
Podložené nohy na ledě
#244,
Marek Scholz (admin),
pos:4/9,
kat
Pan Hňup má před domem zamrzlý rybník. Led je však tenký. Přesto by se pan Hňup chtěl projít po rybníku. Napadlo ho, že si každou botu podloží čtvercovou destičkou, čímž sníží tlak. Jakou minimální délku strany (v cm) musí mít takový čtverec? Pan Hňup má hmotnost 80 kg a tenký led vydrží tlak maximálně 5 kPa.
Řešení: Zápis: p = 5000 Pa; m = 80 kg; F = 800 N.
Platí p = F/S.
Do vztahu můžeme dát čísla:
5000 = 800 / S
Odtud vyvodíme, že S = 800/5000 = 0,16 m2.
To je čtverec o ploše 1600 cm2.
Plocha čtverce je strana x strana. Jaké číslo musím samo sebou vynásobit, abych dostal 1600? Ano, je to číslo 40.
Čtverec by musel mít stranu o délce 40 cm.
Výsledek: 40 cm
ID: 244;
Tags: ;
Autor: Marek Scholz (admin);
Position: 4/9;















