▮ 1) Z vody do skla #203, pos:4/9, kat
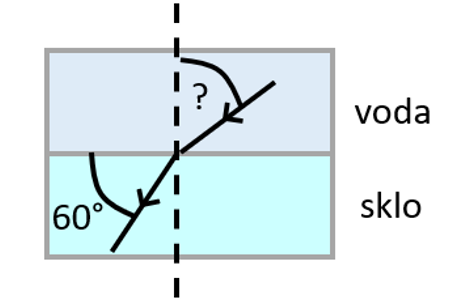
Určete, jaký musí být úhel dopadu na rozhraní voda-sklo, aby paprsek do skla vycházel pod úhlem 60° vůči rovině rozhraní. Index lomu skla je 1,5 a index lomu vody 1,33.
▮ 2) Žárovka a zrcadlo #205, pos:2/9, kat
Máte k dispozici duté zrcadlo o poloměru křivosti 1 metr. Ve vzdálenosti 60 cm od vrcholu zrcadla je žárovka.
a) Zakreslete situaci.
b) Kde se vytvoří obraz? Jaké jsou jeho parametry?
c) Pro jaký interval předmětových vzdáleností vzniká skutečný obraz, pro jaký interval zdánlivý?
d) Pro jaký interval zvětšený obraz, pro jaký zmenšený?
e) Pro jaký interval převrácený a pro jaký přímý obraz?
▮ 3) Čočka #206, pos:5/9, kat
Legolas má spojnou čočku s optickou mohutností 5 D.
Do jaké vzdálenosti musí dát předmět od čočky s ohniskovou vzdáleností f, aby se za čočkou tvořil
a) obraz o stejné velikosti jako předmět
b) dvojnásobně zvětšený obraz
c) poloviční obraz
d) skutečný obraz
e) zdánlivý obraz
f) převrácený obraz
▮ 4) Maximální úhel pro optické vlákno #202, pos:4/9, kat
Jádro optického vlákna má index lomu 1,5, zatímco plášť 1,4.
a) schematicky znázorněte optické vlákno a chod paprsku.
b) Určete, pro jaký interval úhlů dopadu na rozhraní jádra a pláště dochází k totálnímu odrazu.
c) Určete, pod jakým maximálním úhlem může dopadat paprsek na čelo vlákna, aby došlo k jeho totálnímu odrazu uvnitř vlákna.
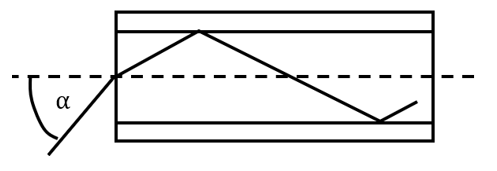
Vložte odpověď na otázku c) maximální úhel.
▮ 5) Zvětšená lampa #204, pos:5/9, kat
Lampa je od stěny 2 metry daleko. Chceme, aby na stěně vzniknul 4x zvětšený obraz lampy. K dispozici máme spojnou čočku.
a) Sestavte zobrazovací rovnici a zakreslete celou situaci do obrázku a sestavte zobrazovací rovnici.
b) Jak daleko od lampy čočku umístíme?
c) Jakou optickou mohutnost musí mít čočka, kterou použijeme?
-
Z vody do skla
Určete, jaký musí být úhel dopadu na rozhraní voda-sklo, aby paprsek do skla vycházel pod úhlem 60° vůči rovině rozhraní. Index lomu skla je 1,5 a index lomu vody 1,33.
Řešení:
Výsledek:
-
Žárovka a zrcadlo
Máte k dispozici duté zrcadlo o poloměru křivosti 1 metr. Ve vzdálenosti 60 cm od vrcholu zrcadla je žárovka.
a) Zakreslete situaci.
b) Kde se vytvoří obraz? Jaké jsou jeho parametry?
c) Pro jaký interval předmětových vzdáleností vzniká skutečný obraz, pro jaký interval zdánlivý?
d) Pro jaký interval zvětšený obraz, pro jaký zmenšený?
e) Pro jaký interval převrácený a pro jaký přímý obraz?
Řešení:
Výsledek:
-
Čočka
Legolas má spojnou čočku s optickou mohutností 5 D.
Do jaké vzdálenosti musí dát předmět od čočky s ohniskovou vzdáleností f, aby se za čočkou tvořil
a) obraz o stejné velikosti jako předmět
b) dvojnásobně zvětšený obraz
c) poloviční obraz
d) skutečný obraz
e) zdánlivý obraz
f) převrácený obraz
Řešení:
Výsledek:
-
Maximální úhel pro optické vlákno
Jádro optického vlákna má index lomu 1,5, zatímco plášť 1,4.
a) schematicky znázorněte optické vlákno a chod paprsku.
b) Určete, pro jaký interval úhlů dopadu na rozhraní jádra a pláště dochází k totálnímu odrazu.
c) Určete, pod jakým maximálním úhlem může dopadat paprsek na čelo vlákna, aby došlo k jeho totálnímu odrazu uvnitř vlákna.
Řešení:
Výsledek:
-
Zvětšená lampa
Lampa je od stěny 2 metry daleko. Chceme, aby na stěně vzniknul 4x zvětšený obraz lampy. K dispozici máme spojnou čočku.
a) Sestavte zobrazovací rovnici a zakreslete celou situaci do obrázku a sestavte zobrazovací rovnici.
b) Jak daleko od lampy čočku umístíme?
c) Jakou optickou mohutnost musí mít čočka, kterou použijeme?
Řešení:
Výsledek: